Пример предварительной таблицы кода Хэмминга
| Разряды двоичных чисел | Символы кода | ||
| 3(k3) | 2(k2) | 1(k1) | |
| m1 | |||
| m2 | |||
| k4 | |||
| m3 | |||
| k5 | |||
| k2 | |||
| k1 |
По предварительной таблице составляется проверочная таблица, в которой выписаны символы кодовой комбинации (4.6) в трех строках, формируемые по следующим правилам.
В первую строку записываются символы, против которых проставлены единицы в младшем (первом) разряде комбинации двоичного кода табл. 4.12. Так, в комбинациях 001, 011, 101 и 111 единицы находятся в младших разрядах, поэтому в первой строке проверочной таблицы (см. табл. 4.14) записывается символ т1,против которого стоит единица в комбинации двоичных чисел 001. Далее в первую строку записывается символы k4, k3 и k1.
Во вторую строку проверочной таблицы записываются символы, против которых проставлены единицы во втором разряде двоичного кода. Так, комбинации 010, 011, 110 и 111 содержат во втором разряде 1, поэтому вторая строка проверочных коэффициентов состоит из символов m2, k3, k2и k1.
В третью строку записываются символы, против которых проставлены единицы в третьем разряде двоичного кода, это символы т3, k3, k2 и k1.
Таблица 4.15
Проверочная таблица кода Хэмминга
| m1 | k4 | k3 | k1 |
| m2 | k4 | k2 | k1 |
| m3 | k3 | k2 | k1 |
Число строк в проверочной табл. 4.15 равно числу контрольных символов т.
В случае кодирования более длинных информационных кодовых комбинаций табл. 4.14 и 4.15 должны быть расширены, так как должны быть записаны четвертая, пятая и т.д. строки проверочных коэффициентов. Для этого нужно лишь увеличить число разрядов двоичного кода в табл. 4.14. Например, для комбинации т1, m2, k11, m3, k10, k9, k8, m4, k7, k6, k5, k4, k3, k2, k1,имеющей одиннадцать информационных символов и четыре контрольных символа, табл. 4.14 будет содержать 15 строк, а табл. 4.15 будет состоять из четырёх строк.
Состав контрольных символов с помощью проверок определяют следующим образом. Суммируют информационные символы, входящие в каждую строку табл. 4.15; если сумма единиц в данной строке четная, то значение символа т,входящего в эту строку, равно 0, если нечетная, то 1. По первой строке табл. 4.15 определяют значение символа т1,по второй – т2,по третьей – m3.
Полученные по табл. 4.15 контрольные символы подставляют в полную кодовую комбинацию (4.6) кода Хэмминга, которая теперь полностью определена.
Пример 4.1
Закодировать кодом Хэмминга, исправляющим одну ошибку, информационную комбинацию двоичного кода 1101.
В информационной комбинации содержится четыре информационных разряда, т.е. k=4.
Согласно табл. 4.13 число контрольных символов m=3, и в соответствии с (4.6) размещаются они на позициях 1, 2 и 4, а информационные символы – на позициях 3, 5, 6 и 7 полной кодовой комбинации, в которой всего семь разрядов, так как n=k+m. Символы информационной части известны, а контрольные символы необходимо определить.
Полную кодовую комбинацию можно записать в виде:
т1m2 k4 m3 k3k2 k1
? ? 1 ?1 0 1
Для определения контрольных символов заполняем табл. 4.15 значениями информационных символов и в полученной таким образом табл. 4.16 суммируем по модулю 2 информационные символы каждой строки.
Таблица 4.16
Проверочная таблица кода Хэмминга,
заполненная информационными символами
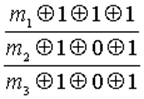
Очевидно, что суммирование информационных символов первой строки даёт 1, суммирование этих символов второй и третьей строк даёт 0. Следовательно, имеем следующий состав контрольных символов: т1 =1, m2 =0, m3=0.
Подставляя контрольные символы на их позиции в (4.6), получим полную кодовую комбинацию кода Хэмминга: 1 0 1 0 1 0 1.
Декодирование кода Хэмминга. Для обнаружения и исправления ошибки выполняются следующие действия.
1. Заполнение проверочной таблицы символами полной кодовой комбинации
Проверочная таблица кода Хэмминга (см. табл. 4.15) заполняется символами полной кодовой комбинации с использованием структуры (4.6) этой комбинации.
2. Суммирование по модулю 2 строк проверочной таблицы
Символы всех строк проверочной таблицы суммируются по модулю 2. Если результат суммирования по всем строкам нулевой, то в принятой комбинации искажений нет. Наличие ненулевого результата означает наличие искажений.
3. Определение места искажения
Место искажения определяется двоичным числом, являющимся результатом суммирования. Для этого столбец результата суммирования читается по вертикали снизу вверх, так что старшим разрядом двоичного числа является результат суммирования последней строки проверочной таблицы, а младшим разрядом – результат суммирования первой строки проверочной таблицы.
4. Исправление искажения
Для исправления искажения полученное двоичное число переводят в десятичное, которое означает номер разряда полной кодовой комбинации, включая контрольные разряды, в котором имеется искажение. Счёт разрядов ведётся слева направо. Принятый символ этого разряда заменяется противоположным, т.е. 0 заменяется на 1 или 1 заменяется на 0. Получается неискажённая кодовая комбинация.
Контрольные символы в соответствии с (4.6) отбрасываются, неискажённая информационная часть обрабатывается.
Пример 4.2
Принята кодовая комбинация 1010111. Известно, что она закодирована кодом Хэмминга, исправляющим одну ошибку. Определить, есть ли в ней искажение, и если есть, то исправить его.
Принятая кодовая комбинация имеет 7 разрядов, поэтому согласно табл. 4.11 в ней имеется 4 информационных символа и 3 контрольных. Структура такой комбинации имеет вид (4.6):
| т1 | m2 | k4 | m3 | k3 | k2 | k1 |
Проверочная таблица семиразрядного кода Хэмминга имеет вид табл. 4.15. Подстановка в неё символов принятой комбинации даёт табл. 4.17.
Таблица 4.17
Проверочная таблица принятой кодовой комбинации примера 4.2
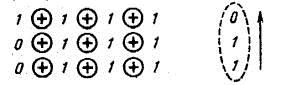
Результат суммирования по модулю 2 строк этой таблицы приведен в правом столбце: первая строка даёт нулевой результат, вторая и третья строки дают единичный результат. Такой результат свидетельствует о наличии искажения.
Для исправления ошибки результат суммирования читается по вертикали снизу вверх. Это даёт двоичное число 110, ему соответствует десятичное число 6. Полученный результат означает, что искажён шестой разряд принятой кодовой комбинации, считая слева направо. Искажён разряд k2.Поэтому принятый символ этого разряда, равный 1, заменяется на символ 0, получена исправленная (неискажённая) кодовая комбинация 1010101. Отбрасываются контрольные символы первой, второй и четвёртой позиций полной кодовой комбинации, неискажённая информационная комбинация имеет вид 1101 (см. пример 4.1).
Итак, для повышения помехоустойчивости кода необходимы дополнительные контрольные символы, которые увеличивают длину кодовой комбинации. Например, семиразрядный код обеспечивает передачу 27=128 кодовых комбинаций, однако количество информационных символов в семиразрядном коде Хэмминга k = 4, т.е. полезных информационных посылок всего Nk =24=16. Остальные 112 кодовых комбинаций из 128 предназначены для обеспечения помехоустойчивости кода, являются запрещенными и не используются.
Выше был рассмотрен код Хэмминга с исправлением одиночной ошибки. Такие коды применяют в том случае, если статистика показывает, что наиболее вероятны одиночные искажения в канале связи. Однако если вероятность искажения двух символов в кодовой комбинации велика, то целесообразно применение кода Хэмминга, позволяющего исправить одиночные ошибки, если была только одиночная ошибка, и, кроме того, обнаружить двойные ошибки, если были две ошибки.
Для построения такого кода число контрольных символов определяется не по табл. 4.13, а по формулам (4.3), (4.4), (4.5).
Имеются и частные приёмы построения кодов Хэмминга с повышенными корректирующими способностями. Например, код Хэмминга, позволяющий исправить единичные ошибки, если была только одиночная ошибка, и, обнаружить двойные ошибки, если были две ошибки, строится на базе кода, исправляющего единичные ошибки. Для этого к полной кодовой комбинации кода Хэмминга добавляется контрольный символ, дополняющий до чётности всю комбинацию, включая этот символ. Контрольный символ должен быть равен единице, если число единиц в закодированной комбинации (4.6) нечетное, и нулю, если число единиц четное.
В табл. 4.18 приводится несколько комбинаций четырехразрядного двоичного кода, закодированных для исправления одиночной ошибки, с добавлением дополнительного контрольного разряда mдоп, с целью проверки этих комбинаций на четность.
При декодировании принятой комбинации возможны следующие варианты.
1. Ошибок нет (прием верен). В таком случае как проверка на чётность расширенной кодовой комбинации, так и проверка по проверочной таблице дают нулевые суммы. Все контрольные разряды, включая mдоп, отбрасываются.
Таблица 4.18
Примеры кодов Хэмминга,
обнаруживающих две ошибки и исправляющих одну ошибку
| Десятичный эквивалент | Позиции, разряды и обозначения кода Хэмминга | mдоп | ||||||
| 23 | 22 | 21 | 20 | |||||
| т1 | m2 | k4 | m3 | k3 | k2 | k1 | ||
| I | ||||||||
| I |
2. Имеется единичная ошибка. В таком случае проверка на чётность расширенной кодовой комбинации показывает наличие ошибки (сумма единиц по модулю 2, входящих в кодовую комбинацию, не дает нуль). Декодирование по проверочной таблице без разряда mдоп указывает на номер искаженного символа, который нужно заменить на противоположный.
3. Имеются две ошибки. Проверка на чётность расширенной кодовой комбинации указывает на отсутствие ошибок, а декодирование по проверочной таблице – на наличие ошибки. В результате декодирования указывается номер позиции, где якобы возникла ошибка, однако её не следует исправлять, а лишь констатировать наличие двух ошибок).
Добавление дополнительного контрольного символа mдоп к закодированной для исправления одиночной ошибки кодовой комбинации увеличивает кодовое расстояние с d=3до d =4, так как r = 2, s = 1, а d = 2 + 1 + 1=4.
4.7.2. Циклические коды
Эти коды широко применяются в аппаратуре передачи данных и системах телемеханики благодаря высокой эффективности [9]. Простота аппаратной реализации на регистрах сдвига и ячейках сумматора по модулю два в своё время обеспечила им широкое применение, а сравнительно небольшая избыточность делает их эффективными в настоящее время.
Кодовая комбинация имеет информационные и контрольные разряды, последние помещаются в конце комбинации, т.е. коды являются систематическими, равномерными, обозначаются (n, k), где n – полное число разрядов, k – число информационных разрядов. Информационной частью служит натуральный двоичный код.
Дата добавления: 2021-11-16; просмотров: 646;











