Примеры инверсного кода
| Информационные символы k | Контрольные символы m | Инверсный код n =k + m |
Декодирование инверсного кода при его приёме осуществляется в два этапа. На первом этапе суммируются единицы в первой половине полной кодовой комбинации. Если сумма единицчётная, то контрольные символы т принимаются без изменений, если нечётная, то символы т инвертируются.
На втором этапе контрольные символы т сравниваются с символами k, и при наличии хотя бы одного несовпадения вся переданная комбинация п = k + m элементов бракуется. Это поэлементное сравнение эквивалентно суммированию по модулю 2. При отсутствии ошибок в обеих половинах символов полной кодовой комбинации их сумма равна нулю.
Пусть передана первая комбинация из табл. 4.12. Ниже показано суммирование для трёх вариантов приема переданной комбинации:
1) 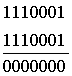 2)
2) 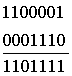 3)
3) 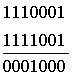
В первом варианте искажений нет и число единиц в информационных символах k четное, поэтому производится суммирование по модулю 2 с неинвертируемыми символами т,что в результате дает нулевую сумму. Во втором варианте число единиц в символах k нечётное, единица в пятом разряде искажена, и символы т инвертированы. В третьем варианте искажение возникло в четвертом разряде группы т. Таким образом, из трех вариантов лишь первый оказался без искажений, а второй и третий должны быть забракованы из-за наличия несовпадения в группах символов k и m.
Корректирующие возможности инверсного кода достаточно велики. Этому способствует метод его построения. Добавление т символов приводит к увеличению минимального кодового расстояния.
После инвертирования корректирующие возможности кода изменяются в зависимости от числа разрядов исходного двоичного кода. Так, если передаются все комбинации обычного двоичного кода с k = 2 (00, 01, 10 и 11), то этот непомехоустойчивый код, превращаясь в инверсный (0000, 0110, 1001 и 1111), увеличивает минимальное кодовое расстояние до dmin =2и позволяет обнаруживать все одиночные ошибки и 67% двойных ошибок.
Действительно, в каждой комбинации может быть С42 = 6 двойных ошибок: так, комбинация 0000 при двойных ошибках примет вид 1100, 0110, 0011, 1001, 1010 и 0101. При этом только второе и четвертое искажения не могут быть обнаружены.
У трёхразрядного двоичного кода (000, 001, .. , 111) после преобразования его в инверсный код кодовое расстояние увеличивается до dmin=3. Это значит, что такой код гарантированно обнаруживает все двойные ошибки. Кроме того, он обнаруживает 80% тройных и четверных ошибок и все пяти- и шестикратные ошибки.
Четырехразрядный двоичный код (0000, 0001,.... 1111) после преобразования его в инверсный код имеет dmin = 4. Он обнаруживает все ошибки во втором, третьем, пятом, шестом и седьмом символах, не обнаруживает 22% четырехкратных ошибок и совсем не обнаруживает восьмикратные ошибки.
Высокие корректирующие возможности инверсного кода достигаются за счет очень большой избыточности. В этом отношении инверсный код значительно уступает другим кодам, о которых будет сказано далее.
4.7. КОДЫ С ОБНАРУЖЕНИЕМ
И ИСПРАВЛЕНИЕМ ОШИБОК
Если кодовые комбинации составлены так, что отличаются друг от друга на кодовое расстояние d = 3, то они образуют корректирующий код, который позволяет по имеющейся в кодовой комбинации избыточности не только обнаруживать, но и исправлять ошибки.
4.7.1. Коды Хэмминга
Для построения кода Хэмминга используется информационная часть в виде двоичного кода на все сочетания с числом информационных символов k, к которой добавляют контрольные символы т. Таким образом, общая длина полной кодовой комбинации n =k + m.
Рассмотрим последовательность кодирования и декодирования по Хэммингу.
Кодирование кодом Хэмминга предусматривает выполнение следующих этапов.
1. Определение числа контрольных символов. Для этого можно воспользоваться следующими рассуждениями. При передаче по каналу с помехами при единичном искажении может быть искажен любой из п символов кода, всего будет n вариантов искажённых комбинаций. Код может быть передан и без искажений. Таким образом, при единичном искажении может быть n + 1 вариантов передачи, включая передачу без искажений. Используя контрольные символы, необходимо различить все п + 1 вариантов. С помощью контрольных символов m можно описать 2m событий. Значит, должно быть выполнено условие
2m ≥ n + 1=k + m + 1. (4.3)
В неравенстве (4.3) по известной величине k находится число контрольных разрядов m, необходимых для построения кода, способного обнаружить и исправить заданное число ошибок.
В табл. 4.13 представлена зависимость между k и т,полученная из неравенства (4.3).
Таблица 4.13
Число контрольных символов в зависимости от числа
информационных разрядов для исправления одной ошибки
| k | |||||||||||||
| m |
Число искажённых кодовых комбинаций зависит от кратности искажения и в общем случае определяется по формуле
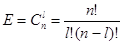 , (4.4)
, (4.4)
где n – число разрядов полной кодовой комбинации,
l – кратность искажения.
Неравенство (4.3) в общем случае записывается в виде
2m ≥ Е+1, (4.5)
где величина Е определяется (4.4).
Формулы (4.4) и (4.5) позволяют определить число контрольных разрядов для искажений произвольной кратности.
2. Размещение контрольных символов. Для удобства обнаружения искаженного символа целесообразно размещать их на местах, кратных степени 2, т.е. на позициях 1, 2, 4, 8 и т.д. Информационные символы располагаются на оставшихся местах. Поэтому, например, для семиэлементной полной кодовой комбинации можно записать
m1, m2, k4, m3, k3, k2, k1, (4.6)
где k4 – старший (четвертый) разряд информационной кодовой комбинации двоичного кода, подлежащий кодированию; k1 – младший (первый) разряд.
3. Определение состава контрольных символов. Какой из символов должен стоять на контрольной позиции (1 или 0), выявляют с помощью проверочной таблицы. Рассмотрим это на примере комбинации (4.6).
Вначале составляется предварительная таблица (табл. 4.14), в которой записаны все кодовые комбинации (исключая нулевую) для трехразрядного двоичного кода на все сочетания и в правом столбце сверху вниз проставлены символы комбинации кода Хэмминга, записанные в последовательности (4.6).
Таблица 4.14
Дата добавления: 2021-11-16; просмотров: 686;











