Математические основы циклических кодов.

Кодовая комбинация представляется в виде многочлена (полинома) с фиктивной переменной x.

G(x) = a_n-1x^n-1 + a_n-2x^n-2 + ... + a₁x + a₀x⁰,

где коэффициенты а_i, i=0, 1, 2, … n-1 принимает значения 0 или 1.

Если а_i = 0, то этот член опускается.

Многочлен G(x) легко переводится в двоичный код. Например,

G(x) = x⁷ + x⁵ + x³ + x² + 1→10101101.

Если многочлен G(x)имеет старшую степень 7, то он называется многочленом 7-й степени.

Над многочленами можно выполнять математические действия по определенным правилам.

Сложение и вычитание равносильны и выполняются по mod 2.

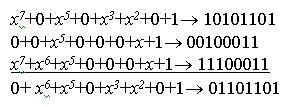
Умножение многочлена на x повышает степень каждого слагаемого многочлена на 1, умножение на хⁿ повышает степень каждого слагаемого на n. Это соответствует передвижению кодовых комбинаций на одну или «n» позиций в сторону старшего разряда.

Например, (х³+х+1)х³=х⁶+х⁴+х³ → 1011000.

В двоичном коде произведение получается из умножаемого двоичного числа приписыванием к нему справа количества нулей, равного величине степени «n».

Умножение многочлена на многочлен выполняется по правилам алгебры, при этом операция сложения выполняется по mod 2.

Деление многочлена на многочлен выполняется по правилам алгебры, при этом операция вычитания равносильна сложению по mod 2. Деление производится до тех пор, пока степень остатка не станет меньше степени делителя (число разрядов остатка меньше числа разрядов делителя).

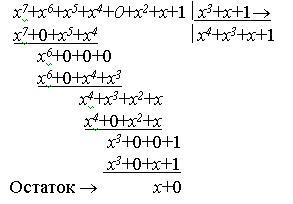
Среди множества многочленов существуют неприводимые, которые не могут быть представлены в виде произведения многочленов низших степеней. Они аналогичны простым числам, которые делятся без остатка лишь сами на себя и на 1.

Для построения многочлена F(x) циклического кода производят следующие преобразования и операции:

1. Многочлен G(x) информационной части умножают на x^n-k; при этом степень многочлена G(x) повышается на величину «n-k».

2. К произведению (x^n-k)*(G(x)) добавляют остаток R(x) от деления x^n-k * G(x) на образующий многочлен P(x).

Это вытекает из следующих преобразований:

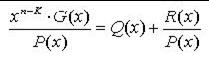, (4.7)

где Q(x)– частное от деления без учета остатка, R(x) – остаток от деления, степень которого меньше степени P(x).

Умножая равенство (4.7) на P(x) получим:

x^n-K * G(x)=Q(x) * P(x)+R(x).(4.8)

Здесь Q(x)*P(x)=F(x) – искомый многочлен циклического кода, поэтому

F(x)= x^n-K * G(x)+ R(x), (4.9)

знак (-) заменен на (+), так как сложение выполняется по mod 2.

Пример 4.3

Найти кодовую комбинацию циклического (7, 4) кода для информационной комбинации 1011 и образующего многочлена P(x)=х³+x²+1.

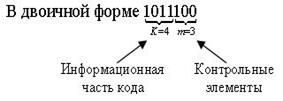
Циклический (7,4) код имеет полное число разрядов n =7, число информационных разрядов k =4, число контрольных разрядов m =3.

Алгебраический многочлен информационной комбинации имеет следующий вид:

G(x)= х³+x+1 → 1011.

Умножение на x^n-k даёт:

G(x)= (х³+x+1)х³= х⁶+х⁴+х³.

Выполняем деление полученного произведения на образующий многочлен:

Таким образом, деление произведения x^n-k * G(x) на образующий полином P(x)даёт остаток R(x)= х², что соответствует двоичному числу 100.

Наконец, многочлен комбинации циклического кода.

F(x)=(х⁶+х⁴+х³)+х².