Принципы построения циклических кодов.

Определенные комбинации циклического кода можно значительно упростить, если применить способ записи натурального двоичного кода с помощью единичной транспонированной матрицы.

Таблица 4.19

Единичная и единичная транспонированная матрицы
четырёхразрядного двоичного кода

Определяющей матрицей натурального двоичного k – разрядного кода является квадратная единичная матрица I_k или единичная транспонированная матрица I_k^T, имеющая k – столбцов и k – строк. Разница между этими матрицами в том, какая из главных диагоналей имеет все элементы, равные 1 (табл. 4.19).

Из матрицы I_k или I_k^T путем сложения нескольких строк по модулю 2 в различных сочетаниях можно получить все ненулевые комбинации кода.

При использовании этого способа записи достаточно многочлены, образуемые строками I_k^T, умножить на x^n-k, разделить на P(x) и остаток приписать в виде дополнительной матрицы C_{(n-k), k} контрольных элементов. Тогда определяющую матрицу C^* циклического (n, k) кода можно записать в следующем виде:

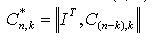. (4.10)

Пример 4.4

Построить циклический (7, 4) код для образующего многочлена P(x)=х³+x²+1.

У этого кода n=7, k=4, m=3. Для построения используем единичную транспонированную матрицу.

Первая строка этой матрицы G(x)=1, поэтому G(x)*x³= x³. Далее выполняем деление на образующий многочлен и для этой строки получаем остаток 101 (табл. 4.20). Здесь же приведены результаты деления, выполняемого для других строк матрицы.

Вторая строка матрицы G(x)= x, поэтому G(x)*x³= x⁴. Деление на образующий многочлен даёт для этой строки остаток 111.

Аналогичные действия для третьей строки дают остаток 011, для четвёртой строки – остаток 110 .

Полученные остатки запишем в форме дополнительной матрицы контрольных элементов (табл. 4.21).

Вместо четырех операций деления можно провести одну, взяв в качестве делимого первую строку единичной матрицы I_k, умноженную на 1000 (х³) (табл. 4.22).

Таблица 4.20