Механизм процесса адсорбции

Адсорбцией называется концентрирование вещества в поверхностном слое в результате его самопроизвольного перехода из объема фазы.

Процесс адсорбции обычно наблюдается в 2-х фазных системах:

· Газ – твердое;

· Жидкость - твердое.

Равновесие в процессе адсорбции определяется двумя процессами:

1. Притяжением молекул (ионов) к поверхности раздела фаз под действием межмолекулярных сил.

2. Тепловым движением, стремящимся восстановить равенство концентраций в поверхностном слое и объеме фазы.

Количественно процесс адсорбции характеризуется числом молей или массой вещества, накапливающегося на границе раздела фаз в расчете на единицу площади или объема твердой фазы.

Фундаментальным вкладом в учение об адсорбции явилась теория Ленгмюра. Эта теория позволяет учесть ограниченность адсорбционного объема или поверхности адсорбента по поглощаемому веществу. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества.

Это положение является основным в теории Ленгмюра и уточняется следующими допущениями:

1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата - образуется мономолекулярный слой;

2) адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна;

3) адсорбированные молекулы не взаимодействуют друг с другом.

Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:

А* + В ↔АВ*

где А* - адсорбционные центры на поверхности адсорбента;

В – адсорбируемые молекулы;

АВ* - образующийся на поверхности комплекс.

По мере увеличения концентрации вещества В реакция сдвига­ется в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного рав­новесия (без учета коэффициентов активности реагирующих веществ) равна:

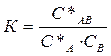(1)

В этом соотношении

С*_АВ=А и С*_А =А∞ - А, (2)

где А – величина адсорбции (количество поглощенного вещества на единице поверхности или массы адсорбента);

А∞ - максимальная емкость адсорбционного слоя.

Подставляя уравнение (2) в уравнение (1), получим:

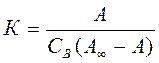
или

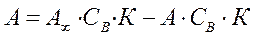
После преобразований:

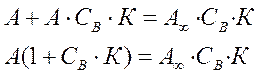
окончательно получим

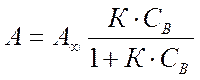(3)

Выражение (3) называется уравнением изотермы адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:

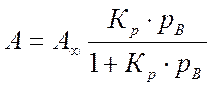, (4)

где РВ – парциальное давление вещества В в газовой смеси.

Необходимо отметить, что константа адсорбционного равнове­сия в уравнении Ленгмюра (К и К_Р) характеризует энергию взаи­модействия адсорбата с адсорбентом. Чем сильнее это взаимодей­ствие, тем больше константа адсорбционного равновесия.

Важны экстраполяционные следствия из соотношений (3) и (4). При малых концентрациях или давлениях, когда С_В ® 0, получаем:

К×С_В ®0 и А = А¥×К×С_В

Величина адсорб­ции линейно растет с увеличением концентрации.

При больших концентрациях и давле­ниях, когда К×С_В >>1 и Кр×р_В >>1, уравнения (3) и (4) пе­реходят в соотношение:

А = А¥ (5)

Соотношения (5) отвечают насыщению, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата.

При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концен­трация свободных центров является общей для равновесной мно­гокомпонентной системы.

В этом случае изотерма адсорбции для i –го компонента запишется следующим образом:

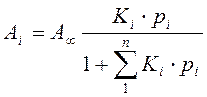(6)

Из уравнения (6) следует, что увеличение парциального дав­ления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия.

Уравнение Ленгмюра можно использовать только при отсут­ствии адсорбции вещества сверх мономолекулярного слоя. Это ус­ловие выполняется достаточно строго при хемосорбции, физиче­ской адсорбции газов при небольших давлениях и температурах выше критической (при отсутствии конденсации на поверхности адсорбента), а часто и при адсорбции из растворов.

В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энер­гию и поэтому остается возможность влияния поверхностных сил на второй, третий и последующие адсорбционные слои. Эта воз­можность реализуется, когда газы и пары адсорбируются при температурах ниже критической, т. е. образуются полимолекуляр­ные слои вещества на поверхности адсорбента, что можно пред­ставить как вынужденную конденсацию пара под действий по­верхностных сил. В результате если в области образования моно­молекулярного слоя величина адсорбции существенно замедляет свой рост с увеличением давления пара, то в области давлений, близкой к давлению насыщенного пара, она резко начинает воз­растать и адсорбция заканчивается объемной конденсацией пара при p = ps (ps-давление насыщенного пара).

Современная же форма уравнения полимолекулярной ад­сорбции — основного уравнения обобщенной теории Ленгмюра — была предложена лишь примерно двадцать лет спустя Брунауэром, Эмметом и Теллером. В соответствии с начальными буквами фамилий авторов обсуждаемая теория получила название теории БЭТ.

В этой теории дополнительным допуще­нием к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, яв­ляется представление об образовании на по­верхности адсорбента «последовательных ком­плексов» адсорбционных центров с одной, дву­мя, тремя и так далее молекулами адсорбата.

Согласно теории БЭТ изотерма полимолекулярной адсорбции описывается уравнением:

,

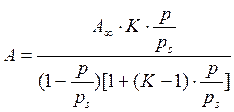где К – постоянная, равная отношению констант адсорбции и конденсации пара (константа конденсации пара величина обратная давлению насыщенного пара).

К=Кр×рs

При уменьшении парциального давления р/рs<<1

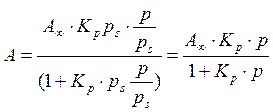
изотерма полимолекулярной адсорбции превращается изотерму Лэнгмюра (мономолекулярная адсорбция).