Числовые характеристики вариационных рядов

Наиболее простыми и часто используемыми числовыми характеристиками выборки являются выборочная средняя 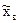, выборочная дисперсия D_в, выборочное среднее квадратическое отклонение (стандарт) s_в, являющиеся аналогами математического ожидания М(Х), дисперсии D(X) и среднего квадратического отклонения s(Х) в теории вероятностей. Наряду с этими числовыми характеристиками определяют моду M_о, медиануM_e вариационного ряда и коэффициент вариации d_в.

Если выборка представлена вариационным рядом распределения (табл.1). указанные числовые характеристики выборки определяются по следующим формулам:

а) выборочная средняя 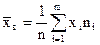; (1)

б) выборочная дисперсия 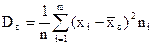; (2)

в) выборочное среднее квадратическое отклонение 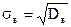(3)

где n - объем выборки, i = (1, …m)- номер варианты, х_i - числовые значения варианты, n_i; - частоты.

Модой М_o вариационного ряда является значение х_i, варианты ряда, имеющее наибольшую частоту n_i.

Медианой М_е вариационного ряда называется значение признака х_i, - приходящегося на середину ранжированного ряда наблюдений. При нечетном объеме выборки n медиана равна серединному значению элемента, а при четном- полусумме двух серединных значений.

Коэффициент вариации равен процентному отношению выборочного среднего квадратического отклонения к выборочной средней:

(%),

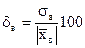где .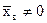

Для интервального вариационного ряда выборочная средняя и дисперсия выборки определяют по формулам:

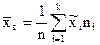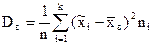(1a); (2a);

где n - объем выборки, i = (1, …k) - номер соответствующего интервала группировки, 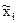- серединные значения интервалов, n_i интервальные частоты.

Для обеспечения необходимой точности расчетов все значения числовых характеристик выборки рекомендуется вычислить на порядок точнее исходных данных, а все промежуточные расчеты на 2 значащие цифры точнее, чем приводимые окончательные результаты.