Вариационные (статистические) ряды
Задачи математической статистики. Генеральная совокупность и выборка
Математическая статистика опирается на теорию вероятностей и занимается разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений.
Если в теории вероятностей предполагались известными вероятности наступления отдельных случайных событий, законы распределения случайных величин и их числовые характеристики, то на практике выводы о закономерностях случайных массовых явлений и процессов приходится делать по данным наблюдения над ними, или проводить соответствующий эксперимент. Поэтому математическую статистику определяют как науку о принятии решений в условиях неопределенности. Используемые в ней основные понятия теории вероятностей (вероятность наступления случайного события, параметры и законы распределения случайных величин и т.д.) выступают в качестве моделей реальных закономерностей.
Одной из задач математической статистики является нахождение характеристик и установление законов распределения случайных величин (СВ) на основе статистической обработки опытных данных.
При статистической обработке обычно используется выборочный метод, основными понятиями которого являются генеральная совокупность и выборка.
Генеральной совокупностью называется общая совокупность всех однородных объектов, из которых производится выборка. Выборочной совокупностью или выборкой называется часть элементов п генеральной совокупности, отобранных случайным образом.
С помощью выборки оценивают генеральную совокупность по вероятностным свойствам. Чтобы оценки были достоверными, выборка должна быть репрезентативной (представительной), то есть ее вероятностные свойства должны быть близкими свойствам генеральной совокупности. Выборка будет репрезентативной, если каждый объект ее отобран случайно из генеральной совокупности. Последняя должна по возможности состоять из однородных объектов.
Вариационные (статистические) ряды
Пусть из генеральной совокупности СВ X извлечена выборка { х1, х2,...хn} объема n, записанная в порядке регистрации. Для изучения закономерностей варьирования (изменения) значений случайной величины опытные данные располагают обычно в порядке не убывания - проводят ранжирование.
Изучаемый признак СВ может быть дискретным, то есть его значения отличаются на конечную величину, или непрерывным, когда значения могут отличаться на сколько угодно малую величину (размер, объем, вес и т.д.).
В случае дискретного признака в ранжированном ряде выделяют группы элементов ni, принимающих одинаковые значения. Наблюдаемые значения х1, х2,...хn называют вариантами, число наблюдений ni (i=1…n) - частотами, а их отношение к объему выборки 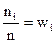 - относительными частотами или частостями.
- относительными частотами или частостями.
Последовательность пар вариант (xi, ni), записанная в виде таблицы (табл. 1) называется вариационным (статистическим) рядом или статистическим распределением.
Таблица 1
| Х | х1 | х2 | … | хm |
| Р | n1 | n2 | … | nm |
где 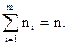
Статистическое распределение непрерывного признака СВ X или дискретного при большом объеме выборки (п > 50) представляют в виде интервальных вариационных рядов, выполняя группировку данных выборок но интервалам. С этой целью весь интервал значений разбивают на ряд частичных непересекающихся интервалов одинаковой длины h и подсчитывают частоту попадания я, значений в каждый частичный интервал:
1. По имеющейся выборке устанавливают наименьшее (xmin) и наибольшее (xmax) значения выборки и размах варьирования R = xmax - xmin;
2. Определяют длину интервалов. При выполнении контрольной работы рекомен-дуется h находить по формуле Стерджеса 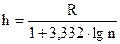 , округляя полученный результат до ближайшего целого числа. За начало первого интервала принять величину хнач=
, округляя полученный результат до ближайшего целого числа. За начало первого интервала принять величину хнач= 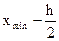 .
.
Промежуточные интервалы получают путем прибавления к концу предыдущего интервала найденной длины число h.
3. Рассматривая выборку, определяют частоты ni попадания в каждый интервал значений СВ. В интервал включаются значения хi большие или равные началу интервала, а равные концу интервала, - не входят. Для таких подсчетов удобно использовать специальную таблицу.
4. По полученным данным составляется интервальный ряд распределения - ранжированный в порядке возрастания (или убывания) ряд вариант с соответствующими им частотами. Для последующих расчетов целесообразно в него включить также относительные частоты wi и середины интервалов 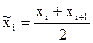 , (табл. 2).
, (табл. 2).
Таблица 2
| № интервалов | Границы интервалов | Частоты ni | Относительные частоты 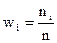
| Середины интервалов 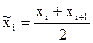
| |
| xi | xi+1 | ||||
| х1 | х2 | n1 | w1 | 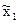
| |
| х2 | х3 | n2 | w2 | 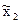
| |
| х3 | х4 | n3 | w3 | 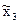
| |
| … | … | … | … | … | … |
| k-1 | хk-1 | хk | nk-1 | wk-1 | 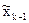
|
| k | хk | хk+1 | nk | wk | 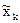
|
Контроль: 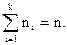
Дата добавления: 2021-11-16; просмотров: 664;











