Дискретное преобразование Лапласа.

Служат для упрощения описания импульсных систем, которые включают в себя и непрерывные элементы. Непрерывные сигналы преобразуют в фиктивные дискретные сигналы. Тогда вместо обычных дифференциальных уравнений используют и дискретные преобразования Лапласа.

Поскольку выходной сигнал импульсного элемента зависит от непрерывного входного сигнала только в дискретные моменты времени, а именно в начале каждого периода повторения импульсов, если замкнуть непрерывную функцию U(t) на его вход дискретной функцией, значение которой в моменты n·Tn, (n=0,1,2,3,…) совпадают со значением непрерывной функции, а в остальное время равно нулю. Такую дискретную функцию называют решетчатой функцией.

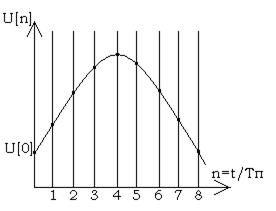
График решетчатой функции, записанной в нормированной форме.

τ=t/Tn ; Tn=1 U[n] .

Дискретным преобразованием Лапласа называется функциональное преобразование решетчатых функций в виде U[n], U[n·Tn], которое определяется выражением:

D{U[n·Tn]}=U*(p)=∑U(n·Tn)·e^-p·n·Tn .

Для нормированной решетчатой функции:

D{U[n]}=U*(g)=∑U(n)·e^-g·n , где

g=p·Tn - безразмерная переменная.

Производят Z-преобразование.

z{U[n]}=U*(z)=∑U[n]·z^-n .

Так как дискретные преобразования Лапласа аналогично обычному преобразованию Лапласа, то при его использовании применяют аналогичные правила и теоремы, которые позволяют найти решетчатую функцию, исследовать установившиеся и переходные процессы в импульсных системах, решить разностные уравнения.

Скорость изменения решетчатой функции характеризуется ее первой разностью:

ΔU[n]=U[n+1]-U[n] .

Ускорение – второй разностью решетчатой функции:

Δ²U[n]=ΔU[n+1]-ΔU[n] .

Реакурентное соотношение – к-ой разностью решетчатой функции:

Δ^кU[n]=Δ^к-1U[n+1]-Δ^к-1U [n] .

Соотношение между решетчатой функцией и ее разностями различных порядков определяет уравнение в конечных разностях, так называемое разностное уравнение.

Уравнение линейных разностей с постоянными коэффициентами можно записать в виде:

в_кΔ^кx[n]+ в_к-1Δ^к-1x[n]+…+ в₀x[n]=U [n] .

U[n] – известная функция, которую можно записать в память, извлечь из памяти и использовать.

X[n] – искомая функция, представляющая собой решение разностного уравнения.

Решением разностного уравнения является функция обратного z-преобразования, которая представляется в виде суммы элементарных членов:

x[z]=c₀+c₁ ·z^-1+c₂·z^-2+=3+1· z^-1+1,2·z^-2

Поскольку: z=e^q=e^pTn

z-n=e^-pTn·n=e^-pT

При цифровом управлении строят цифровые корректирующие устройства (ЦКУ).

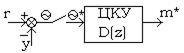
ЦКУ обеспечивает умножение на некий коэффициент числового значения, поступающего на вход ЦКУ, причем коэффициент будет различен в разные моменты времени, в этом и заключается цифровая коррекция или регулирование, то есть

m[0]=k₀·Ө*[0]= k₀·r[0]- k₀·y[0]

m[1]=m[Tn] = k₁· Ө*[Tn]

m[2Tn]= k₂· Ө*[2·Tn]

- - - - -

m[nTn]= k_n· Ө*[n·Tn]

M[z]= k₀· Ө*[0·Tn]·z^-0+ k₁·Ө*[1·Tn]·z^-1 + k₂·Ө*[2·Tn]·z^-2+ k_n·Ө*[n·Tn]·z^-n= ∑k_j· Ө*[j·Tn]·z^-j

Аналогично можно расписать для ошибки:

Ө*[z]=∑Ө*[j·Tn]·z^-j

Тогда передаточная функция ЦКУ будет записана:

D[z]=M*[z]=∑k_j· Ө*[j·Tn]·z^-j =∑m[j·Tn]·z^-j

Ө*[z] ∑Ө*[j·Tn]·z^-j ∑Ө*[j·Tn]·z^-j

Пусть:

Ө*[0]=Ө*[0· Tn]=1 m*[0]=1

Ө*[1· Tn]=0,8 m*[1· Tn]=0,25

Ө*[2· Tn]=0,39 m*[2· Tn]=-0,568

Ө*[3· Tn]=0,082 m*[3· Tn]=-0,432

D[z]=1+0,25·z^-1 -0.568·z^-2-0,432·z^-3

1+0.8·z^-1+0,39·z^-2+ 0,082·z^-3

Цифровую передаточную функцию реализуют на ЭВМ, используя рекурентные соотношения:

m*[n]=Ө*[n]+0,25·Ө*[n-1] -0,568·Ө*[n-2]-0,432· Ө*[n-3]-0,8 ·m*[n-1] -0,39·m*[n-2]-0,082· m*[n-3]

t_пп=4·T_п (4 периода дискретности).

В ЭЛУ ЭВМ реализует подпрограмму:

Проверка аварийного режима и готовности оборудования с последовательным опросом датчиков и конечных выключателей:

- подача шихты или испаряемого материала;

- втягивание слитка;

- расчет отклонения

- программа проверки температуры;

- программа проверки давления.

Рассмотрим фрагмент подпрограммы расчета момента окончания процесса напыления.

Подпрограмма реализует алгоритм, интегрируя во времени скорости подачи испаряемого материала:

Q[i·T_п]=Q[(i-1)·T_п]+T_п·ν_п [i·T_п] , 1≤i≤n

В индукционных нагревательных установках управляющая ЭВМ на каждом шаге квантования решает электромагнитную и тепловую задачи – моделирует переходные процессы.

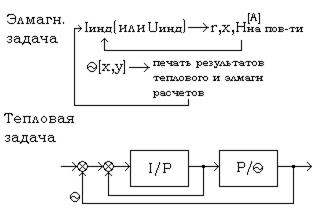
Важной проблемой при построении ЦСУ является период квантования T_п-?

T_п=f (свойств материала, Ө_технич), если в течении любого цикла опроса решается М_задач (М_з=10) и для каждой задачи необходимо к=10³ машинных команд. Тогда быстродействие машин для плавления печью N[опер/сек].

N> М_з·к/Т_у=10·10³/67≈150оп/сек

Для управления высокочастотной сваркой:

N> М_з·к/Т_у=10·10³/6,7·10^-3≈1,5·10⁶оп/сек

Время цикла определяется тем рабочим временем, за которое управляемая переменная Ө_p изменяется на допустимую погрешность регулирования ΔӨ_p.

Температура расплава может быть выражена в зависимости:

Ө_p=Р· 1 ·t , T_п<T_р

M·c

Р - управляющая переменная;

M- масса;

c- теплоемкость.

Пусть для сталеплавильной печи:

c=0,67·10³Дж/кг·°С , Р=500кВт , М=1000кг

ΔӨ=50°С

T_п<ΔӨ_р·М·с=50·1000·0,67·10³

Р 500·1000

Пусть время нагрева под ВЧ сварочной трубы от исходной температуры до температуры плавления:

t_н=0,2с

ΔӨ_р=50°С

T_п< t_н ·ΔӨ_р=0,2·50=6,7·10^-3

Ө_плавл 1500

МП с высокой производительностью - это дорогие устройства и часто на практике проектируют двух уровневые и супервизорные ЦУ.

В этом случае ЭВМ вычисляет лишь уставки локальным регулятором.

Эти регуляторы могут быть реализованы как в аналоговом виде (операционный усилитель) на вход которых уставка подается в цифроаналоговых преобразованиях, так и в виде аппаратных или МП устройств, обладающих большим быстродействием.

В аварийных режимах локальный регулятор может управляться вручную.