Устойчивость предельных циклов.

В нелинейной системе существует два типа предельных циклов:

1. В устойчивом предельном цикле амплитуда колебания возвращается в прежнее состояние после возмущения.

2. Неустойчивый предельный цикл, если под действием какого-либо фактора амплитуда колебаний меняется и с течением времени колебания затухнут, либо наоборот, амплитуда увеличивается и будет неограниченно возрастать.

Рассмотрим неустойчивый предельный цикл в следующей системе:

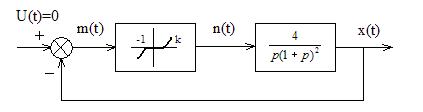
В этой системе зона нечувствительности описывается функцией:

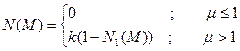
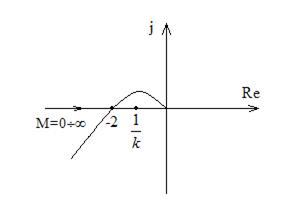
При m>>1, N(M)®1

Допустим, что в системе существует предельный цикл в точке M=K и .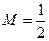

При увеличении М рабочая точка сместиться влево, это будет соответствовать увеличению амплитуды на выходе системы, сигнал которой будет увеличиваться.

Если рабочая точка сместиться вправо от –2 , то амплитуда будет меньше, т.е. цикл является неустойчивым.

Неустойчивый предельный цикл соответствует устойчивой работе системы.

В данном случае это происходит по следующим причинам:

При малых сигналах m(t) 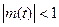. Если он меньше 1, то n(t)=0 и система определенно является устойчивой.

Для несколько больших сигналов амплитуды эффективный коэффициент усиления будет малым и система будет устойчивой.