Определение и свойство нелинейных систем.

Линейная система – система, для которой применим принцип суперпозиций.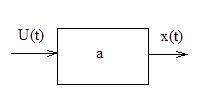

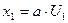
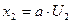
Нелинейной называется система для которой не применим принцип суперпозиций.

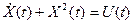
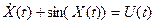
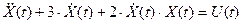
Стационарная система- система, параметры которой не зависят от времени.

Преобразование Лапласа не может быть использовано для решения линейных диф. уравнений с переменными параметрами и для нелинейных д.у. любого вида.

Описание объекта передаточной функцией подразумевает то, что он является линейным и стационарным.

Одним из свойств нелинейных систем является то, что их устойчивость может зависеть от входных сигналов и от начальных условий.

При изучении и описании нелинейных систем применяют следующие характеристики:

1. Предельный цикл.

Периодические незатухающие колебания в нелинейной системе называются предельным циклом. В общем случае он не является sin. В нелинейных системах амплитуда незатухающих колебаний не зависит от внешних воздействий и от начальных условий.

2. Частота вынужденных колебаний при периодическом входном воздействии. При подаче на вход н.с. периодического воздействия частота вынужденных колебаний на выходе системы может быть либо субгармоникой или гармоникой.

Например, если частота входных колебаний – 10 Гц, то колебание может быть

3 Гц – субгармоника

30 Гц – гармоника.

3. Явление скачкообразного резонанса.

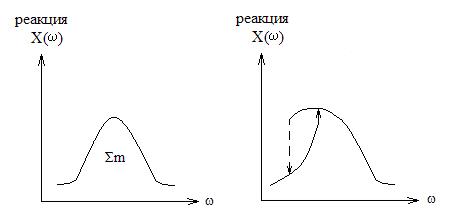
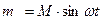, где М=const.

4. Множество состояний равновесия.

Если линейная система устойчива, то при снятии входного воздействия все переменные состояния с течением времени стремятся к нулю.

В устойчивой нелинейной системе могут существовать несколько различных состояний равновесия отличных от нуля и к ним система стремится при отсутствии входного воздействия.

Метод описывающей функции (гармонической линеаризации) для представления нелинейного звена, как элемента САУ.

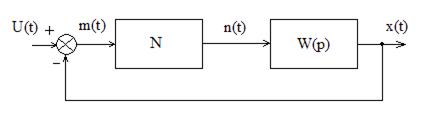
В этом методе определения приближенного описания нелинейности полагают, что входной сигнал нелинейности является синусоидальным. Тогда выходной сигнал нелинейности будет периодическим, но не синусоидальным.

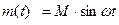
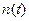- не sin.

Такой сигнал можно представить в виде ряда Фурье.

;

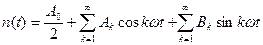Коэффициенты выражаются:

;

;

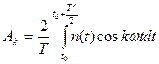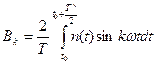Для многих технических случаев ограничиваются допущением, что 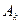=0 , т.к. при этом нелинейность симметрична относительно оси. В этой методике полагают , что w(t) соответствует фильтру низких частот. Передаточная функция пренебрежимо мала для сигналов всех гармоник, кроме первых. Т.е. выходной сигнал при этом можно записать в виде:

.

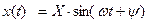И сигнал нелинейности аппроксимируют выражение

;

;

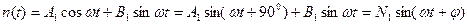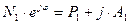Отсюда следует, что сигнал N(t) можно аппроксимировать sin. той же частоты, но имеющей другую амплитуду и фазу. Поэтому нелинейность можно представить в виде комплекса коэффициента усиления.

;

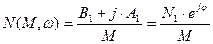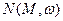- эквивалентный коэффициент усиления называется описывающей функцией и изображается на схемах следующим образом:

N= ;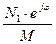

Описывающая функция N(M,w) в общем случае зависит как от амплитуды, так и от частоты входной амплитуды. Эта функция играет роль эквивалентного коэффициента усиления только при очень жестких ограничениях:

1. Входной сигнал нелинейности является sin-ым.

2. Линейная система , следующая за нелинейностью является фильтром низких частот и ослабляет все высшие гармоники на столько, что их влиянием можно пренебреч.