Характеристика схемы последовательного включения звеньев.

Построение производится от выхода к входу для нескольких рабочих точек системы.

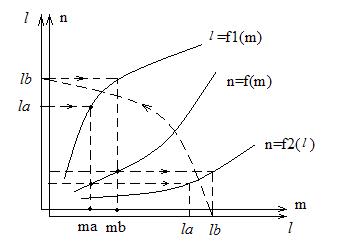
Исследование систем методом фазовой плоскости.

Представим, что некоторый процесс описывается д.у.

;

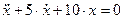Представление д.у. высокого порядка системой n-х уравнений первого порядка называется описанием системы в пространстве состояний(переменные состояния).

Из него видно, что система будет колебательной.

Обозначим 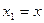- перемещение,

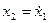- скорость,

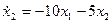- ускорение.

Переменных состояний столько, сколько элементов в системе запасает существующую энергию.

Эти переменные состояния можно изобразить графически , как в функции времени, так и в функции друг друга.

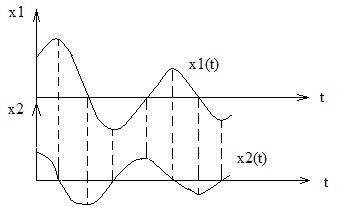
Изображение в фазовой плоскости имеет вид:

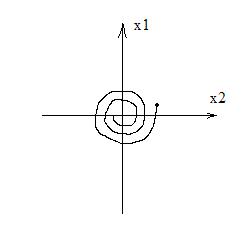
Методом фазовой плоскости исследуются системы второго порядка, однако, применяется прием, когда системы высокого порядка исследуются сначала ,как система второго порядка, с учетом лишь двух динамических звеньев с самыми большими постоянными времени, затем строится фазовая траектория с наиболее динамичным звеном первой группы, потом третьей и.т.д.

Рассмотрим систему релейного управления методом фазовой плоскости:

Элемент Пельтье

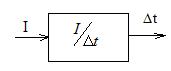
где : ;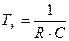

.

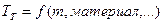Если предположить, что эти постоянные времени равны 1.

Тогда:

;

;

; ;

;

;

;

;

;

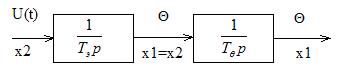
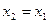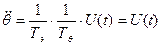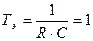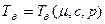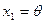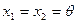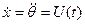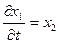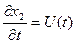Найдем соотношения производных, чтобы освободиться от параметра t:

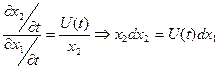
U(t) в данном выражении – постоянная, на отрезке времени на котором рассматривается движение системы в фазовой плоскости.

Проинтегрируем уравнение:

;

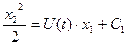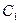-единственная постоянная интегрирования, полученная из начальных условий.

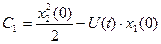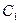; ­ при ­

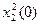
Для 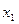может быть получено выражение:

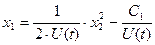
Если U(t)=const, то уравнение можно представить семейством парабол.

1) Пусть U(t)=-U, тогда

;

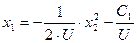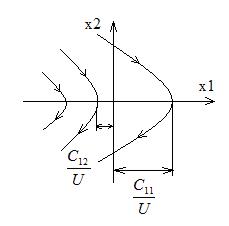
2) Пусть U(t)=U, тогда

;

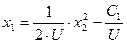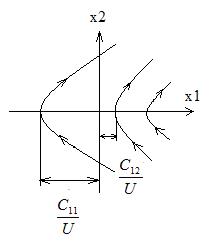
Точка, описывающая движение в системе фазовых координат( 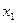; 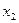) располагается на одной из изображенных парабол, в зависимости от начальных условий 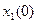, 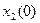и от знака управляющего сигнала U. Величина сигнала будет определять скорость движения описывающей точки по данной параболе, а знак сигнала: <0; >0, то движение идет по часовой стрелке.

Рассмотрим замкнутую систему управления температурой элемента Пельтье.

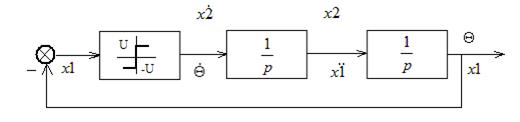
В такой системе при разных напряжениях и для разных начальных условий получим семейство траекторий.

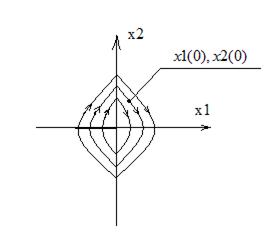
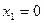-уравнение линии переключения.

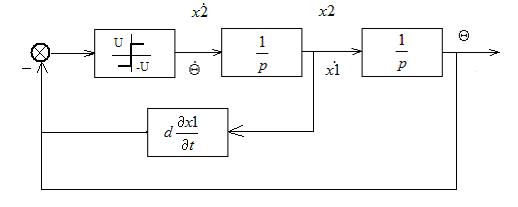
1) Входной сигнал на линейную часть системы:

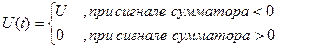
Движение системы описывается теми же параболическими уравнениями.

2) Если до введения обратной связи по скорости 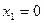, то уравнение примет вид: ;

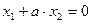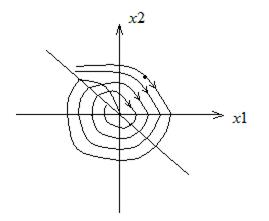
Фазовая траектория будет иметь вид: