Основные положения анализа метода описывающей функции.

В нелинейной системе возникает предельный цикл, если входной сигнал на n будет приблизительно синусоидальным и будет полностью восстанавливаться в замкнутом контуре, т.е. будет обеспечен петлевой коэффициент усиления равный 1.

Задача анализа- определить существует ли амплитуда М и частота w такие, при которых коэффициент усиления разомкнутого контура от входа нелинейности к той же самой точке равен 1 при условии, что нелинейность заменена её описывающей функцией.

Формально ;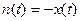

В системе предельный цикл возникает, если:

;

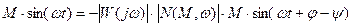Для определения наличия искомой рабочей точки в этом выражении приравнивают амплитуды:

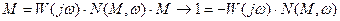
По аналогии с характеристическим уравнением в системе записывают :

, если это уравнение удовлетворяется, то можно предсказать существование предельного цикла.

В действительности существование предельного цикла можно установить только путем испытаний реальной системы.

Поскольку N(M,w) в общем случае является комплексной функцией, то уравнение не поддается непосредственному решению. Для нахождения M и w , для соответствующих единичному петлевому усилению прибегают к решению графоаналитическим методом, т.е. строятся кривые для левой и правой частей следующего уравнения:

;

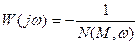Если при некотором значении w две кривые пересекаются, то уравнение имеет решение и в нелинейной системе возможно существование предельного цикла.

Рассмотрим систему с нелинейностью в виде идеального реле (компаратора).

Согласно таблице описывающих функций правая часть уравнения

;

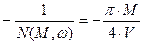График этой функции строится изменением М от 0 до w.

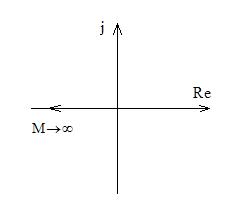
График функции 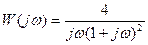строится подстановкой различных значений w от 0 до .

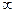При построении можно убедиться , что действительная ось пересекается этим годографом при w=1.

;

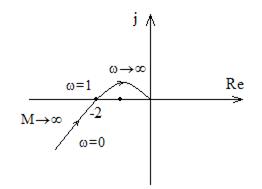
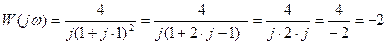Таким образом точки пересечения графиков соответствуют условиям:

, откуда ;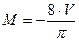

Метод описывающей функции предсказывает существование в данной системе предельного цикла при котором сигнал выхода определяется выражением:

;

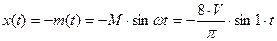При этом выходной сигнал реле имеет вид прямоугольных колебаний с амплитудой V. Значит существуют способы, для избежания предельных циклов в системе, надо найти способы, чтобы на этой частоте (в полосе рабочих частот системы) недопустить усиление амплитуды , в 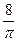- раз.