Интегральные показатели качества.
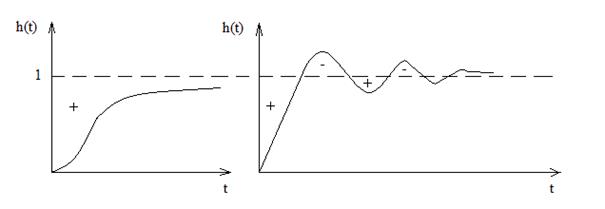
Интегральные показатели качества основаны на том, что качество регулирования тем выше чем меньше площадь между кривой переходного процесса h(t) и заданным значением регулируемой величины. Наибольшее применение получили следующие показатели :
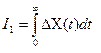 , где
, где 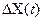 =1(t)-h(t)
=1(t)-h(t)
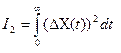
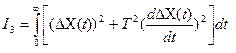 .
.
Т – постоянное время некоторой экспоненты по которой должна изменяться регулируемая величина согласно техническому заданию.
Чем меньше заштрихованная площадь , тем предпочтительнее переходные процессы. Интеграл I может применяться только для оценки качества неколебательных монотонных процессов. С помощью квадратичного интегрального критерия 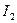 оценивают качество колебательного перехеходного процесса (п.п.). При этом знаки площадей не приводятся во внимание.
оценивают качество колебательного перехеходного процесса (п.п.). При этом знаки площадей не приводятся во внимание.
В большинстве случаев выбор изменяемых параметров системы по MIN интегралу 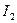 приводит к системе с большой колебательностью. И если это неприемлимо, то используется критерий
приводит к системе с большой колебательностью. И если это неприемлимо, то используется критерий 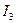 , интеграл которого состоит из двух частей: 1) Определяет площадь, ограничиваемую квадратом отклонения регулируемой величины, а вторая площадь, ограничиваемую квадратом скорости изменения отклонения. Если при одной и той же площади п.п. замедлить п.п. во времени, то уменьшится вторая часть
, интеграл которого состоит из двух частей: 1) Определяет площадь, ограничиваемую квадратом отклонения регулируемой величины, а вторая площадь, ограничиваемую квадратом скорости изменения отклонения. Если при одной и той же площади п.п. замедлить п.п. во времени, то уменьшится вторая часть 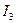 , поэтому MIN
, поэтому MIN 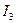 =MIN
=MIN 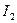 будет существовать при более медленном колебательном п.п.
будет существовать при более медленном колебательном п.п.
Указанные интегралы применяются не только для оценки динамических свойств в САУ и ЭТУ, но и реализуются эти интегралы в виде блоков адаптивных систем , которые формируют параметры звена обратной связи для соответствующей подстройки системы, в зависимости от условий работы ЭТУ.
Чувствительность.
Проблема изменения характеристик системы из-за изменения ее параметров называется проблемой чувствительности. Мерой чувствительности считается – отношение процентного (относительного) изменения передаточной функции системы к процентному отношению этой функции.
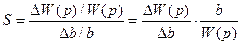 .
.
Функция чувствительности вычисляется как предел выражения S при стремлении Db к нулю. Коэффициент чувствительности можно записать так:
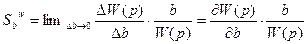 .
.
Зависимость 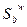 от параметра P (переменная преобразования Лапласа) создает трудности е6е интерпретации.
от параметра P (переменная преобразования Лапласа) создает трудности е6е интерпретации.
Если в этих выражениях заменить P на jw, то можно представить функцию чувствительности в виде технической характеристики. Тогда функция чувствительности преобретает смысл как чувствительность на частотах в полосе пропускания системы (wс).
Т.к. система не пропускает сигналы при частоте w>wс, то чувствительность на этих частотах не представляет интереса.
Получим полезные характеристики.
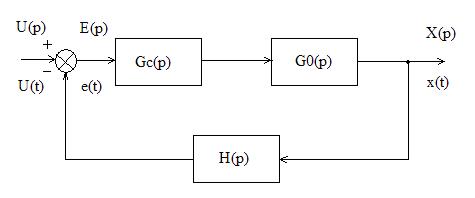
Передаточная функция замкнутой системы :
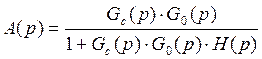 .
.
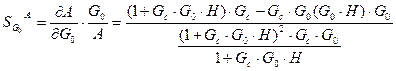
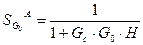
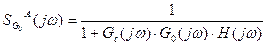
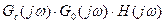 -коэффициент усиления контура на данной частоте.
-коэффициент усиления контура на данной частоте.
Цель проектирования в САУ – сделать систему наименее чувствительной к изменению любых ее параметров . Коэффициент усиления контура в рабочей полосе частот системы желательно увеличить для уменьшения чувствительности системы к изменениям параметров объекта.
Одной из функций регулятора 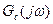 как раз является увеличение коэффициента усиления, но при сохранении устойчивости замкнутой системы.
как раз является увеличение коэффициента усиления, но при сохранении устойчивости замкнутой системы.
Определим чувствительность системы к изменению параметров датчика:
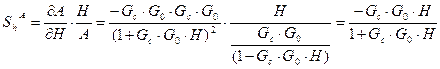 .
.
Знак минус указывает, что увеличение Н приводит к уменьшению чувствительности, чтобы чувствительность системы по отношению к датчику была малой , необходимо, чтобы коэффициент усиления контура также был малым, но уменьшение коэффициента усиления контура делает систему более чувствительной к вариации параметров объекта. Чтобы снять противоречие конструкторы выбирают высококачественный датчик со стабильными характеристиками. (В отношении объекта этого сделать нельзя).
В полученных выражениях 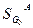 и
и 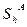 и сами передаточные функции звеньев изменяются, потому что изменяется их какой-либо параметр.
и сами передаточные функции звеньев изменяются, потому что изменяется их какой-либо параметр.
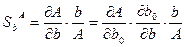
Дата добавления: 2021-11-16; просмотров: 445;











