Определение характеристик случайной функции по опытным данным.

Пусть над случайным процессом X(t) проведено n опытов и получено n реализаций (рис. 6.6).

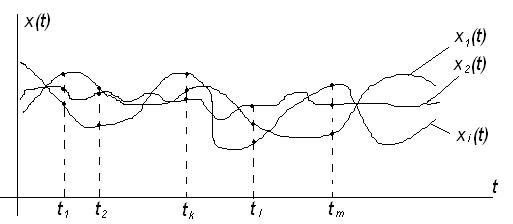
Рисунок 6.6 – Реализации случайного процесса X(t)

Требуется определить: оценку математического ожидания случайного процесса 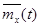; оценку дисперсии случайного процесса 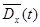; оценку корреляционной функции .

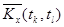Значения, которые принимают реализации случайного процесса X(t), сведем в таблицу 6.2.

Таблица 6.2

x(t) t	t1	t2	…	tk	…	tl	…	tm
x1(t)	x1(t1)	x1(t2)	…	x1(tk)	…	x1(tl)	…	x1(tm)
…	…	…	…	…	…	…	…	…
xi(t)	xi(t1)	xi(t2)	…	xi(tk)	…	xi(tl)	…	xi(tm)
…	…	…	…	…	…	…	…	…
xn(t)	xn(t1)	xn(t2)	…	xn(tk)	…	xn(tl)	…	xn(tm)
			…		…		…

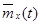
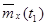
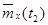
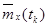
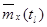
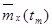
Оценки математического ожидания 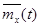в сечениях случайного процесса 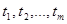находятся как средне – арифметические значения столбцов, т.е.

.

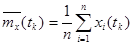Оценки дисперсии 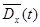в сечениях случайного процесса 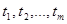находятся как средне – арифметические значения квадратов центрированных значений столбцов, т.е.

.

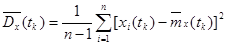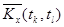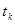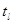Оценки корреляционного момента в парах сечений определяются как средне – арифметические значения произведений центрированных значений столбцов и , т.е.

.

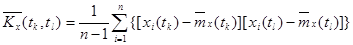По значениям оценок математического ожидания 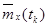в сечениях случайного процесса 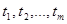строят график функции математического ожидания 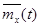случайного процесса (рис.6.3). Для определения степени статистической связи значений случайного процесса между собой и средней величины разброса их по оценкам корреляционного момента 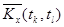составляют таблицу 6.3.

Таблица 6.3

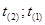
	t1	t2	…	tk	…	tl	…	tm
t1			…		…		…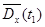
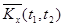
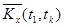
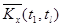
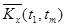
t2			…		…		…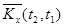
…	…	…	…	…	…	…	…	…
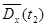
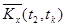
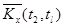
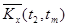
tk			…		…		…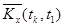
…	…	…	…	…	…	…	…	…
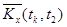
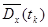
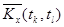
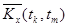
tl			…		…		…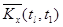
…	…	…	…	…	…	…	…	…
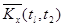
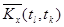
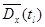
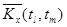
tm			…		…		…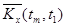

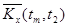
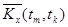
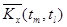
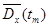
При этом требуемая точность отображения функции математического ожидания и корреляционной функции может достигаться увеличением количества сечений m.