Математическое ожидание и дисперсия случайной функции.

Математическим ожиданием случайного процесса X(t) называется неслучайная функция 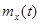, которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайного процесса

.

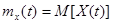Из определения математического ожидания случайного процесса вытекает, что если известна одномерная плотность вероятности 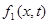, то

.

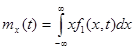Рисунок 6.3 – График функции математического ожидания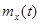

Дисперсией случайного процесса X(t) называется неслучайная функция 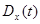, которая при каждом значении аргумента t равна дисперсии соответствующего сечения случайного процесса.

.

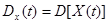Из определения дисперсии случайного процесса вытекает, что если известна одномерная плотность вероятности 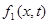, то

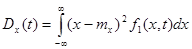или (6.5)

Если случайный процесс представляется в виде 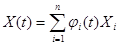, то

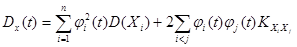. (6.6)

Дисперсия случайного процесса характеризует разброс или рассеивание реализаций относительно функции математического ожидания.

Если реализации случайного процесса представляют собой ток или напряжение, то дисперсию 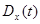трактуют как разность между мощностью всего процесса и мощностью средней составляющей тока или напряжения в данном сечении, т.е.

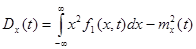. (6.7)

В ряде случаев вместо дисперсии случайного процесса используется среднее квадратичное отклонение случайного процесса

.

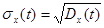Математическое ожидание и дисперсия случайного процесса позволяют выявить вид средней функции, около которой группируются реализации случайного процесса, и оценить их разброс относительно этой функции. Однако внутренняя структура случайного процесса, т.е. характер и степень зависимости (связи) различных сечений процесса между собой, остается при этом неизвестной (рис. 6.4).

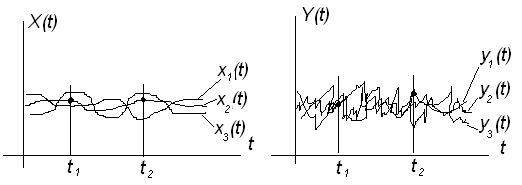
Рисунок 6.4 – Реализации случайных процессов X(t) и Y(t)