ВРЕМЯ ЗАМЕДЛЕНИЯ НЕЙТРОНОВ И ЕГО ДИСПЕРСИЯ

Время замедления нейтронов и его дисперсия — важнейшие характеристики процесса нестационарного замедления нейтронов в веществе.

Полное время замедления нейтронов 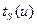определяется следующим образом:

,

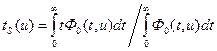где 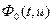— энергетически-временное распределение замедленных нейтронов от начального импульса высокой энергии, инжектированного в среду.

Выражение для времени замедления имеет следующий вид:

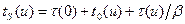. (8.151)

Все три слагаемых в этой формуле имеют ясный физический смысл. Первый член 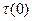есть время свободного пробега при на­чальной энергии (u = 0) до первого столкновения в среде, которым начинается процесс замедления. Величина 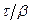соответствует промежутку времени, в течение которого нейтрон, сохраняя заданное значение конечной энергии, движется в среде, пока последующее столкновение не выведет его из рассматриваемого энергетического интервала. Величина

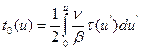. (8.152)

Интеграл в (8.152) может быть вычислен аналитически. Это возможно благодаря экспоненциальному росту с летаргией времени свободного пробега

,

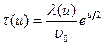вследствие чего основной вклад в величину интеграла дает окрестность верхнего предела. Поэтому все функции, слабо изменяющиеся с летаргией (по сравнению с экспонентой), могут быть вынесены за знак интеграла со значением в верхнем пределе:

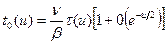, (8.152')

так что

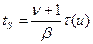. (8.151)

Среды, для которых 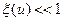(исключение составляют среды с высоким водородосодержанием), характеризуются совпадением полного времени замедления с временем собственно замедления. Рисунок 2.26 иллюстрирует высокую точность, с которой расчетные значения времени собственно замедления согласуются с экспериментально измеренными величинами (по данным многих исследователей).

Из выражения (8.152) вытекает, что время замедления при u>> 1 зависит лишь от конечной энергии нейтронов, следовательно, временное распределение замедленных нейтронов определяется заключительной стадией процесса замедления и позволяет получать полезную информацию о взаимодействии с веществом не только надтепловых, но и тепловых нейтронов. Хотя в области тепловых энергий расчеты с использованием формулы ) для среднего изменения летаргии 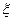неправомерны[5], в случае воды расчетные значения 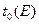хорошо согласуются с экспериментальными данными. Таким образом, величина замедляющей способности воды не изменяется при переходе от надтепловых энергий к тепловым.

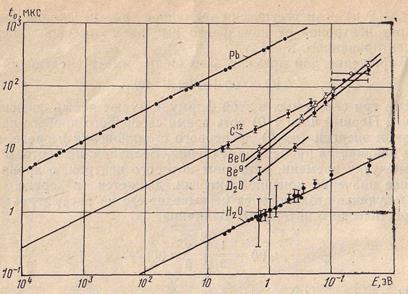
Рис.8.14. Зависимость времени собственно замедления от энергии нейтронов в некоторых веществах. Сводка экспериментальных данных различных исследователей: 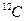- Ж. Коппеля и др., А. Такахаши и К. Сумиты; Рb - А. И. Исакова (ФИАН); 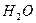- М. Крауха, Дж. де Юрена, А. Накаямы, А. Шуклы и А. Волтнера, Е. Мёллера и Н. Шостранда; и ВеО - И. Ф. Жежеруна (ИАЭ).

Рис.8.15. Зависимости времен замедления нейтронов до энергии индиевого резонанса (1,46 эВ) в песчанике (1) и известняке (2) от водонасыщенной пористости т (по Д.А.Кожевникову).

На рис.8.15 приведена зависимость от водородосодержания времени замедления надтепловых нейтронов в песчанике и известняке.

В приближении Грюлинга — Гертцеля дисперсия времени замедления определяется выражением

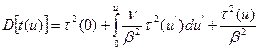. (8.152)

Вычисляя выступающий интеграл аналогично (48), и пренебрегая очень малой поправкой за первый пробег, находим

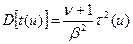. (8.152')

Времена замедления, вычисленные в приближениях Вигнера и Грюлинга — Гертцеля, отличаются не более чем на 15%. В тех же приближениях величины дисперсий различаются более чем в два раза, причем они изменяются качественно различно при изменении водородосодержания замедлителя (рис.8.16). Величина дисперсии в приближении Вигнера монотонно убывает с ростом т, а вприближении Грюлинга — Гертцеля сначала растет и достигает максимума при 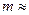0,03 %, после чего убывает, сохраняя заметное различие с вигнеровским значением во всем диапазоне 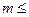40 % (это различие обусловлено неасимптотическим поведением функции Плачека). Таким образом, при количественных оценках нестационарного замедления нейтронов в горных породах приближением Вигнера пользоваться нельзя.

Поскольку время замедления определяется конечной энергией нейтронов, при которой определяющим является взаимодействие с водородом (упругое рассеяние) , оно в однородных средах сильно зависит от водородосодержания, и слабо — от минерального состава матрицы. В системе скважина-пласт (рис.2.28) дополнительно необходимо учитывать наличие водорода в скважине, а при изучении реального коллектора — также наличие остаточной водо- нефтенасыщенности, химически и кристаллизационно связанного водорода в матрице и цементе (нижняя граница пористости превышает величину полной водоудерживающей способности коллектора).

Рис.8.16. Время замедления нейтронов до энергии 5 эВ в зависимости от размера зонда в заполненной водой необсаженной скважине диаметром 160 см. Пласт кварцевого песчаника m = 0 (1) и m =5% (2); диаметр прибора 100 мм. (по данным А.И.Пшеничнюка; расчет методом Монте-Карло).