Оценка адекватности трендовых моделей
Как указывалось ранее, реальный временной ряд содержит систематическую составляющую, которую мы и описываем с помощью трендовой модели, и случайную составляющую Et:
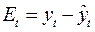 . (5.7)
. (5.7)
Если систематические компоненты временного ряда определены правильно, то остаточная компонента E должна обладать следующими свойствами:
случайностью колебаний уровней остаточной последовательности;
соответствием распределения случайной компоненты нормальному закону распределения;
равенством нулю математического ожидания случайной компоненты;
независимостью значений уровней случайной последовательности.
Далее приводятся процедуры проверки указанных свойств остаточной последовательности (случайной компоненты).
Проверка случайности колебаний уровней остаточной последовательности производится по критерию серий. Ряд из величин Et располагают в порядке возрастания их значений и находят медиану Em полученного вариационного ряда, т. е. срединное значение при нечетном n или среднюю арифметическую из двух срединных значений при n нечетном. Сравнивая значения этой последовательности Et с Em, необходимо фиксировать знак “+”, если Et > Em, и знак “–” при Et < Em. В случае Et = Em это значение опускается. Таким образом, получается последовательность, состоящая из плюсов и минусов, общее число которых не превосходит n. Последовательность подряд идущих плюсов или минусов называется серией. Чтобы последовательность Et была случайной, протяженность самой длинной серии не должна быть слишком большой, а общее число серий – слишком малым.
Обозначим протяженность самой длинной серии kmax, а общее число серий – ν. Выборка признается случайной, если выполняются условия (5.8) и (5.9):
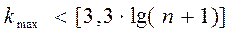 , (5.8)
, (5.8)
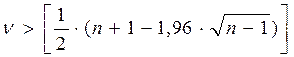 (5.9)
(5.9)
Квадратные скобки означают целую часть числа.
Проверка независимости значений случайной компоненты может осуществляться по ряду критериев, наиболее распространенным из которых является критерий Дарбина-Уотсона. Расчетное значение этого критерия определяется по формуле (5.10)
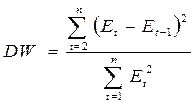 . (5.10)
. (5.10)
Далее по таблицам распределения Дарбина - Уотсона (приложение В) при заданном уровне значимости a, числе наблюдений n и числе независимых переменных (в парной регрессии это 1) находятся два критических значения, меньшие двух: нижнее dl - граница признания положительной автокорреляции остатков и верхняя du - граница признания отсутствия корреляции. По этим значениям рассчитываются интервалы, в пределах которых H0 принимается, отвергается или не может быть принята, или отвергнута (имеется неопределенность):
Таблица 5.1 - Уровни критерия Дарбина - Уотсона
| Значение DW | Вывод |
| (4-dl) < DW < 4 | гипотеза Hо отвергается, есть отрицательная корреляция |
| (4-du) < DW < (4-dl) | неопределенность |
| du < DW < (4-du) | гипотеза Hо принимается |
| dl < DW < du | неопределенность |
| 0 < DW < dl | гипотеза Hо отвергается, есть положительная корреляция |
Примечание: оценка автокорреляции производится только применительно к линейным уравнениям регрессии.
Если остаточная последовательность удовлетворяет всем перечисленным выше требованиям, необходимо оценить показатели точности.
В качестве таких показателей, как уже было указано в разделе 2, наиболее часто используют:
средний коэффициент аппроксимации (среднюю относительную погрешность);
остаточную ошибку (Dост, σост);
коэффициент детерминации.
Если остаточная последовательность не удовлетворяет хотя бы одному из перечисленных выше требований, необходимо выбрать другой вид уравнения тренда и повторить исследование.
Дата добавления: 2018-05-10; просмотров: 893;











