Процедуры определения наличия тренда временного ряда

Для определения наличия тренда в исходном временном ряду применяются различные методы: исследование автокорреляционной функции, критерий серий, критерий тренда. В работе рекомендуется использовать метод проверки разностей средних уровней, осуществляющий проверку стационарности исследуемого временного ряда. Реализация этого метода состоит из четырех этапов [7].

На первом этапе исходный временной ряд y₁, y₂, …, y_n разбивается на две, примерно, равные по числу уровней части: в первой – n₁ первых уровней, во второй – n₂ остальных уровней исходного ряда. При этом следует отметить, что n₁ + n₂ = n.

На втором этапе для каждой из этих частей вычисляются средние значения и оценки дисперсии:

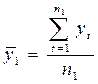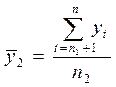, , (5.3)

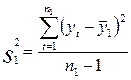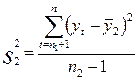, . (5.4)

Третий этап заключается в проверке равенства дисперсий обеих частей ряда с помощью F-критерия Фишера, которая основана на сравнении наблюдаемого значения этого критерия с критическим значением F_кр., которое определяется по справочникам или таблицам Excel (категории статистические: F_кр=FРАСПОБР(α, ν₁, ν₂), если s₁² > s₂² или F_кр=FРАСПОБР(α, ν₁, ν₂), если s₂² > s₁², где ν₁ = n₁ –1, ν₂ = n₂ –1, α – заданный уровень значимости). Если F_набл. < F_кр, то принимается основная гипотеза о равенстве дисперсий. В противном случае гипотеза о равенстве дисперсий отклоняется и делается вывод, что тренда нет.

На четвертом этапе проверяется гипотеза об отсутствии тренда по t-критерию Стьюдента. Расчетное значение критерия Стьюдента определяется по следующей формуле:

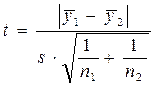, (5.5)

где .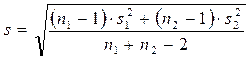

Значение критерия t сравнивается с критическим t_кр, которое определяется по таблицам распределения Стьюдента (приложение Б) по значению уровня значимости α и по числу степеней свободы k (k = n₁ + n₂ – 2). Если значение критерия t меньше t_кр, то принимается гипотеза о равенстве математических ожиданий, что говорит об отсутствии тренда. В противном случае, гипотеза о равенстве математических ожиданий отклоняется и делается вывод о наличии тренда.

5.3. Процедуры сглаживания уровней временного ряда

Поскольку реальные временные ряды, отражающие тенденции развития экономических явлений, всегда сопровождаются воздействием случайных составляющих, то для того, чтобы выявить тенденцию развития исследуемого процесса, в том числе и для целей прогнозирования хода развития процесса, производят сглаживание (выравнивание) временных рядов.

Методы сглаживания временных рядов делятся на две группы:

механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней (метод укрупнения интервалов и метод скользящих средних);

аналитическое выравнивание с использованием кривой, проведенной между конкретными уровнями ряда так, чтобы она отражала тенденцию изменения ряда и освобождала его от случайных колебаний.

При решении практических задач рекомендуется проводить процедуры аналитического выравнивания временного ряда, т.е. подбора аналитической функции, характеризующей зависимость уровней ряда от времени (тренда). Наиболее часто для моделирования этой зависимости используются полиномиальные, экспоненциальные, логарифмические, степенные кривые роста, вид которых приведен ниже:

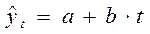- полином первой степени;

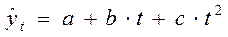- полином (парабола) второй степени;

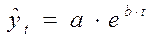- экспоненциальная кривая роста;

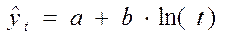- логарифмическая кривая роста;

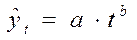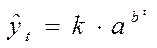, - степенная кривая роста.

На практике обычно отбирают две-три кривые роста для дальнейшего исследования и построения трендовой модели временного ряда. Выбор наилучшего уравнения можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации 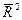(2.15) и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации.

После выбора моделей роста необходимо определить их параметры. Параметры полиномиальных кривых оцениваются методом наименьших квадратов (МНК), суть которого заключается в том, что сумма квадратов отклонения фактических уровней ряда y_t от соответствующих уровней ряда 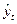, полученных по кривой роста, была наименьшей:

. (5.6)

В данном случае на основе МНК также образуется система нормальных уравнений, решая которую получают значения параметров отобранных регрессионных моделей.

Для полинома первой степени система нормальных уравнений имеет вид:

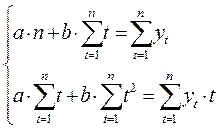
Аналогичным образом можно получить систему для полинома второй и более степеней. Для определения параметров экспоненциальных и степенных кривых путем эквивалентных преобразованиями приводят их к линейному виду, например, путем логарифмирования.

Для оценки тесноты взаимосвязи факторов нелинейных регрессионных моделей используется выражение корреляционного отношения (коэффициента детерминации), которое будет рассмотрено в следующем подразделе пособия.