Исследуемого явления
Рассмотрим метод расчета индексов сезонности по отношению к тренду. Исходные данные динамики объема продаж молочной продукции по кварталам 2013-2015г. представлены в таблице 5.5.3
Произведем расчет значений сезонной компоненты методом скользящей средней и построение мультипликативной модели временного ряда.
Общий вид мультипликативной модели следующий:
Y = T · S · E, (5.12)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (Е) компонент.
Таблица 5.5.3 – Данные объема продаж молочной продукции
| Год | Квартал | Время, t | Объем продаж продукции ( 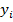 ), тонн ), тонн
|
| I | 9738,3 | ||
| II | 8558,4 | ||
| III | |||
| IV | 9349,8 | ||
| I | 10322,3 | ||
| II | 8994,8 | ||
| III | |||
| IV | 14422,8 | ||
| I | 15160,5 | ||
| II | 16398,1 | ||
| 𝛴 |
Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени, разделив полученные суммы на 4. Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты (!).
Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (таблица 5.5.4).
Таблица 5.5.4 - Выравнивание уровней ряда методом скользящей средней
| t | yt | Скользящая средняя квартальная | Центрированная скользящая средняя квартальная | Оценка сезонной компоненты |
| 9738,3 | - | - | - | |
| 8558,4 | 8806,63 | - | - | |
| 8952,63 | 8879,63 | 0,85 | ||
| 9349,8 | 9061,72 | 9007,17 | 1,04 | |
| 10322,3 | 10066,72 | 9564,22 | 1,08 | |
| 8994,8 | 11334,97 | 10700,85 | 0,84 | |
| 12544,53 | 11939,75 | 0,97 | ||
| 14422,8 | 14395,35 | 13469,94 | 1,07 | |
| 15160,5 | - | - | - | |
| 16398,1 | - | - | - |
Для расчета сезонной компоненты Si используются ее оценки (коэффициенты).
Для рассмотренного примера найдем средние за каждый период оценки сезонной компоненты. Сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. Число периодов одного цикла равно 4.
Таблица 5.5.5 - Расчетная таблица составляющих сезонной компоненты 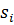
| Показатели | I | II | III | IV |
| - | - | 0,85 | 1,04 | |
| 1,08 | 0,84 | 0,97 | 1,07 | |
| - | - | |||
| Всего за i-й квартал | 1,08 | 0,84 | 1,83 | 2,11 |
| Средняя оценка сезонной компоненты | 1,08 | 0,84 | 0,61 | 0,7 |
| Скорректированная сезонная компонента, Si | 1,336 | 1,041 | 0,753 | 0,870 |
Для данной модели имеем:
1,079 + 0,841 + 0,608 + 0,703 = 3,231
Корректирующий коэффициент: k = 4/3,231 = 1,238
Скорректированные значения сезонной компоненты Si получаются при умножении ее средней оценки на корректирующий коэффициент k.
Проверяем условие равенства суммы значений сезонной компоненты:
1,336 + 1,041 + 0,753 + 0,870 = 4
Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины T · E = Y/S, которые содержат только тенденцию и случайную компоненту.
Предполагая, что фактические уровни у имеют линейный тренд, и, ведя счет времени от начала ряда (t=1,2, 3, ...n), подсчитываем все необходимые суммы (таблица 5.5.6).
Таблица 5.5.6 – Данные расчета параметров уравнения регрессии
| t | yt | 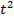
| 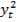
| yt * t |
| 7288,76 | 53126051,9 | 7288,76 | ||
| 8224,64 | 67644630,27 | 16449,27 | ||
| 10064,24 | 101288958,87 | 30192,72 | ||
| 10744,59 | 115446194,04 | 42978,36 | ||
| 7725,86 | 59688985,48 | 38629,32 | ||
| 8644,02 | 74719023,71 | 51864,1 | ||
| 15401,74 | 237213649,05 | 107812,19 | ||
| 16574,37 | 274709792,12 | 132594,97 | ||
| 11347,08 | 128756242,15 | 102123,73 | ||
| 15758,6 | 157585,99 | |||
| Итого: 55 | 111773,9 | 1360926980,57 | 687519,42 |
По этим суммам и определяем параметры а и b, решая систему нормальных уравнений:
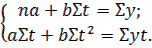
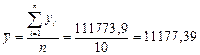 – среднее значение
– среднее значение 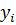 .
.
Найденные значения сумм подставим в систему нормальных уравнений:
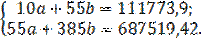
Значения параметров уравнения a и b составят: a = 6326,53, b = 881,98.
Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T · E) с помощью линейного тренда: ŷt = 6326,53+881,98∙t.
Подставляя в это уравнение значения t = 1,...,10, найдем теоретические значения уровней ряда (ŷt) для каждого момента времени, после чего, умножим значения ŷt на соответствующие значения сезонной компоненты (таблица 5.5.7).
Таблица 5.5.7 - Расчет величин индексов сезонности по отношению к тренду
| t | yt | Si | y t / Si | ŷt | ŷt Si | E = yt / (ŷt Si) | (yt - ŷt Si)2 |
| 9738,3 | 1,34 | 7288,76 | 7208,5 | 9631,07 | 1,01 | 11498,99 | |
| 8558,4 | 1,04 | 8224,64 | 8090,48 | 8418,8 | 1,02 | 19488,96 | |
| 0,75 | 10064,24 | 8972,45 | 6757,71 | 1,12 | 676167,07 | ||
| 9349,8 | 0,87 | 10744,59 | 9854,43 | 8575,19 | 1,09 | 600015,86 | |
| 10322,3 | 1,34 | 7725,86 | 10736,4 | 14344,59 | 0,72 | 16178825,02 | |
| 8994,8 | 1,04 | 8644,02 | 11618,38 | 12089,86 | 0,74 | 9579421,19 | |
| 0,75 | 15401,74 | 12500,35 | 9414,79 | 1,23 | |||
| 14422,8 | 0,87 | 16574,37 | 13382,33 | 11645,13 | 1,24 | 7715472,69 | |
| 15160,5 | 1,34 | 11347,08 | 14264,3 | 19058,12 | 0,8 | 15191405,54 | |
| 16398,1 | 1,04 | 15758,6 | 15146,28 | 15760,93 | 1,04 | 405984,51 | |
| 10,01 | 55153441,82 |
Определение прогнозных значений 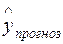 уровней временного ряда (объемов продаж анализируемого предприятия) по мультипликативной модели осуществляется с помощью выражений (5.13):
уровней временного ряда (объемов продаж анализируемого предприятия) по мультипликативной модели осуществляется с помощью выражений (5.13):
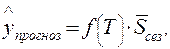
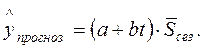 (5.13)
(5.13)
Подставляя соответствующие значения t и сезонных компонент (на основе данных таблицы 5.5.7), получаем прогнозные значения показателей предприятия на III, IV кварталы 2015 года, а также I и II кварталы 2016 г.:
III квартал 2015 года 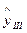 = (6326,53+881,98*11) * 1,336 = 21413,83 тонн;
= (6326,53+881,98*11) * 1,336 = 21413,83 тонн;
IV квартал 2015 года 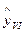 = (6326,53+881,98*12) * 1,041 = 17603,61 тонн;
= (6326,53+881,98*12) * 1,041 = 17603,61 тонн;
I квартал 2016 года 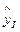 = (6326,53+881,98*13) * 0,753 = 13397,58 тонн;
= (6326,53+881,98*13) * 0,753 = 13397,58 тонн;
II квартал 2016 года 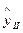 = (6326,53+881,98*14) * 0,87=16246,60 тонн.
= (6326,53+881,98*14) * 0,87=16246,60 тонн.
Ниже представлены примеры для самостоятельного решения заданий по рассматриваемой теме.
Пример № 5.1. Имеются данные о количестве вагонов, отправленных с одной
станции (шт)
| Месяцы | |||
| Январь | |||
| Февраль | |||
| Март | |||
| Апрель | |||
| Май | |||
| Июнь | |||
| Июль | |||
| Август | |||
| Сентябрь | |||
| Октябрь | |||
| Ноябрь | |||
| Декабрь |
Пример № 5.2. Имеются данные о реализации картофеля на рынках города (тонн)
| Месяцы | |||
| Январь | |||
| Февраль | |||
| Март | |||
| Апрель | |||
| Май | |||
| Июнь | |||
| Июль | |||
| Август | |||
| Сентябрь | |||
| Октябрь | |||
| Ноябрь | |||
| Декабрь |
Пример № 5.3. Имеются данные доходов предприятия ОАО «РСУ №3» по комплексному техническому обслуживанию лифтового оборудования, (млн.руб)
| Месяцы | |||||||||
| Январь | 0,47 | 0,32 | 2,5 | 1,5 | 3,8 | 3,6 | 0,76 | 2,6 | 1,5 |
| Февраль | 0,5 | 0,47 | 1,2 | 2,1 | 2,8 | 0,9 | 1,4 | 2,6 | |
| Март | 0,63 | 0,85 | 3,8 | 1,5 | 1,5 | 0,59 | 3,7 | 1,5 | |
| Апрель | 0,89 | 0,92 | 4,8 | 2,4 | 0,98 | 1,5 | 2,8 | ||
| Май | 5,6 | 4,1 | 3,1 | 2,6 | 5,1 | ||||
| Июнь | 0,98 | 6,8 | 5,2 | 3,7 | 4,5 | ||||
| Июль | 0,98 | 1,5 | 4,7 | 4,3 | 4,3 | 2,1 | 0,89 | 3,3 | 3,6 |
| Август | 0,99 | 3,9 | 3,6 | 3,3 | 1,2 | 0,67 | 4,1 | 2,8 | |
| Сентябрь | 0,99 | 0,91 | 2,6 | 2,1 | 2,4 | 1,4 | 1,3 | 1,5 | |
| Октябрь | 0,95 | 0,95 | 1,3 | 0,91 | 1,2 | 2,3 | |||
| Ноябрь | 0,9 | 0,83 | 1,2 | 4,3 | 3,6 | 2,5 | 0,42 | 2,7 | 1,7 |
| Декабрь | 0,75 | 0,75 | 1,1 | 2,2 | 1,6 | 0,47 | 2,1 | 0,9 |
Пример № 5.4. Динамика количества договоров по ОСАГО по месяцам в 2004-20011гг. (млн.ед.)
| Месяцы | ||||||||
| Январь | 3,8 | 2,9 | 2,2 | 2,4 | 2,5 | 2,2 | 2,1 | 2,1 |
| Февраль | 1,6 | 1,6 | 1,7 | 1,9 | 2,3 | 2,2 | 2,1 | 2,3 |
| Март | 1,6 | 2,0 | 2,4 | 2,5 | 3,0 | 3,0 | 3,1 | 3,2 |
| Апрель | 2,2 | 2,6 | 2,9 | 3,7 | 3,4 | 3,5 | 3,7 | 4,0 |
| Май | 1,6 | 2,3 | 3,0 | 3,0 | 3,6 | 3,1 | 3,4 | 3,7 |
| Июнь | 1,5 | 2,3 | 2,5 | 3,1 | 3,1 | 3,1 | 3,4 | 3,6 |
| Июль | 2,2 | 2,5 | 2,8 | 2,8 | 3,3 | 3,1 | 3,3 | 3,5 |
| Август | 2,1 | 2,5 | 2,7 | 3,2 | 3,1 | 3,0 | 3,1 | 3,4 |
| Сентябрь | 1,9 | 2,1 | 2,3 | 2,7 | 3,0 | 3,0 | 3,2 | 3,2 |
| Октябрь | 2,0 | 2,0 | 2,4 | 2,7 | 3,1 | 2,8 | 3,0 | 3,2 |
| Ноябрь | 1,6 | 1,9 | 2,2 | 2,7 | 2,6 | 2,7 | 3,0 | 3,2 |
| Декабрь | 4,5 | 4,0 | 4,0 | 3,8 | 3,7 | 3,5 | 3,6 | 3,9 |
Пример № 5.5. Динамика сборов по ОСАГО по месяцам в 2004-2011гг., (млрд.руб)
| Месяцы | ||||||||
| Январь | 7,8 | 5,8 | 4,7 | 5,1 | 5,4 | 4,9 | 5,2 | 5,3 |
| Февраль | 3,0 | 3,1 | 3,6 | 4,0 | 5,1 | 5,0 | 5,5 | 5,8 |
| Март | 3,1 | 3,9 | 5,0 | 5,9 | 6,4 | 6,8 | 7,7 | 7,9 |
| Апрель | 4,0 | 4,7 | 5,7 | 6,7 | 7,5 | 8,3 | 9,1 | 9,5 |
| Май | 2,7 | 4,0 | 5,7 | 6,3 | 7,4 | 7,5 | 8,0 | 8,7 |
| Июнь | 2,4 | 4,1 | 5,0 | 6,3 | 6,9 | 7,8 | 8,2 | 8,9 |
| Июль | 4,0 | 4,6 | 5,3 | 5,9 | 7,4 | 8,0 | 8,3 | 8,5 |
| Август | 3,7 | 4,6 | 5,5 | 6,4 | 6,7 | 7,3 | 8,0 | 9,5 |
| Сентябрь | 3,5 | 4,0 | 5,0 | 6,1 | 6,7 | 7,7 | 8,1 | 9,5 |
| Октябрь | 3,5 | 3,9 | 5,2 | 5,8 | 6,8 | 7,2 | 7,6 | 9,7 |
| Ноябрь | 3,1 | 3,9 | 4,7 | 6,0 | 6,2 | 6,8 | 7,7 | 9,9 |
| Декабрь | 8,6 | 7,6 | 8,4 | 8,1 | 7,9 | 8,6 | 9,1 | 12,4 |
Вопросы для самопроверки по 5 разделу
1. Перечислите основные составляющие уровней временного ряда.
2. Что характеризует детерминированная компонента в уравнении тренда?
3. Что отражает стохастическая компонента в уравнении тренда?
4. Что отражает циклическая (сезонная) компонента в уравнении тренда?
5. Сущность процедуры определения наличия тренда уровней временного ряда.
6. Процедура подтверждения гипотезы об отсутствии тренда уровней временного ряда по t-критерию Стьюдента.
7. Сущность процедуры проверки случайности колебаний остаточной погрешности уровней временного ряда.
8. Сущность основных подходов по выявлению сезонности уровней динамических (временных) рядов.
9. В чем сущность критерия Дарбина – Уотсона?
10. Укажите наиболее оптимальный период для исследования сезонной составляющей временного ряда.
11. Особенности коррекции прогнозных значений временных рядов на основе аддитивных и мультипликативных моделей.
Дата добавления: 2018-05-10; просмотров: 1082;











