Одномерный корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ - один из наиболее широко распространенных и гибких приемов обработки статистических данных. Данный метод начинает свой отсчет с 1795 г., когда английский исследователь Фрэнсис Гальтон предложил теоретические основы регрессионного метода, а в 1801 г. рассчитал с его помощью траекторию полета планеты Церера. Им же введен в статистику термин «корреляция». Можно также назвать французского кристаллографа Огюста Браве, немецкого физика Густава Теодора Фехнера, английского экономиста и статистика Фрэнсиса Эджуорта, впервые высказывавших в середине—конце XIX в. идеи о количественном измерении связей явлений. В разное время над теорией анализа работали известные в области теоретической статистики ученые Карл Фридрих Гаусс (Германия), Адриен Мари Лежандр (Франция), Карл Пирсон (Англия) и др.
Корреляционно-регрессионный анализ состоит в построении и анализе экономико-математической модели исследуемого явления в виде уравнения регрессии (корреляционной связи), характеризующего зависимость признака от определяющих его факторов.
Наиболее широкое распространение в эконометрических исследованиях получили линейные регрессионные модели вида (2.1)
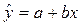 , (2.1)
, (2.1)
где y – результативная (зависимая) переменная (фактор-результат);
x – независимая переменная (фактор-признак);
a,b – параметры модели.
Основными этапами эконометрического исследования являются следующие:
выбор формы уравнения взаимосвязи исследуемых факторов;
определение параметров уравнения регрессии;
оценка тесноты взаимосвязи (корреляции) исследуемых факторов;
оценка адекватности (статистической значимости) уравнения регрессии;
оценка статистической значимости параметров уравнения регрессии.
Кроме указанных этапов, прикладные исследования могут включать этапы, связанные с проведением аналитического прогноза единичных значений результативной переменной, а также оценкой точности и достоверности прогноза.
Параметры регрессионной модели, как правило, оцениваются методом наименьших квадратов (МНК), суть которого заключается в том, что сумма квадратов отклонения фактических значений результативного признака (yi) от соответствующих теоретических значений ( 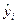 ), полученных на основе выбранной модели, должна быть минимальной:
), полученных на основе выбранной модели, должна быть минимальной:
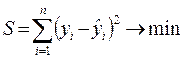 . (2.2)
. (2.2)
В данном случае на основе МНК образуется система нормальных уравнений, решая которую получают значения параметров отобранных регрессионных моделей. Так, для линейной регрессии ( 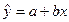 ) система нормальных уравнений имеет вид (2.3):
) система нормальных уравнений имеет вид (2.3):
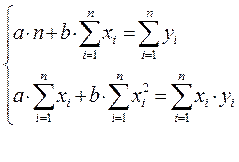 (2.3)
(2.3)
После очевидных и несложных преобразований окончательные выражения для определения параметров линейной регрессии имеют вид:
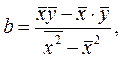 (2.4)
(2.4)
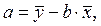 (2.5)
(2.5)
где 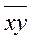 - среднее значение произведения факторов x и y;
- среднее значение произведения факторов x и y;
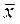 - среднее значение фактора x;
- среднее значение фактора x;
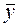 - среднее значение фактора y;
- среднее значение фактора y;
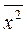 - среднее значение фактора x2;
- среднее значение фактора x2;
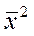 - квадрат среднего значения фактора x;
- квадрат среднего значения фактора x;
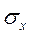 - среднее квадратическое отклонение фактора x;
- среднее квадратическое отклонение фактора x;
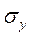 - среднее квадратическое отклонение фактора y.
- среднее квадратическое отклонение фактора y.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора-признака на одну единицу. Кроме того, в ряде случаев для удобства интерпретации параметра b используют коэффициент эластичности. Он показывает средние изменения результативного признака (в %) при изменении факторного признака на 1% и вычисляется по следующей формуле:
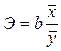 . (2.6)
. (2.6)
Параметр a может не иметь экономического смысла. Формально параметр a – значение фактора y при x=0. Если фактор-признак x не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра a не имеет смысла. Попытки экономически интерпретировать параметр a могут привести к абсурду, особенно при a < 0. Интерпретировать можно лишь знак при параметре a. Если a > 0, то относительное изменение результата происходит медленнее, чем изменение фактора x.
Для определения степени тесноты взаимосвязи исследуемых факторов используется коэффициент корреляции. Выражения для нахождения линейного коэффициента корреляции имеют вид:
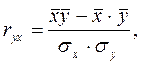 (2.7)
(2.7)
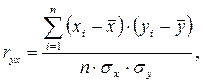 (2.8)
(2.8)
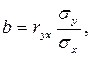 (2.9)
(2.9)
где n - размерность исследуемой выборки (количество наблюдений).
Величина коэффициента корреляции находится в пределах: 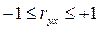 и может принимать следующие значения:
и может принимать следующие значения:
если значение 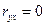 , то корреляция между исследуемыми факторами отсутствует (факторы некоррелированы);
, то корреляция между исследуемыми факторами отсутствует (факторы некоррелированы);
если значение 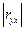 находится в пределах (0…0,3], то между исследуемыми факторами имеется слабая связь;
находится в пределах (0…0,3], то между исследуемыми факторами имеется слабая связь;
если значение 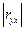 находится в пределах (0,3…0,5], то между исследуемыми факторами имеется умеренная связь;
находится в пределах (0,3…0,5], то между исследуемыми факторами имеется умеренная связь;
если значение 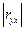 находится в пределах (0,5…0,7], то между исследуемыми факторами имеется довольно устойчивая статистическая связь;
находится в пределах (0,5…0,7], то между исследуемыми факторами имеется довольно устойчивая статистическая связь;
если значение 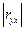 > 0,7 , то между исследуемыми факторами имеется сильная связь (статистически значимая связь, факторы сильно коррелированны);
> 0,7 , то между исследуемыми факторами имеется сильная связь (статистически значимая связь, факторы сильно коррелированны);
если значение 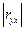 = 1, то между исследуемыми факторами имеется функциональная зависимость.
= 1, то между исследуемыми факторами имеется функциональная зависимость.
Оценка адекватности формы регрессионной модели может быть проведена с помощью:
среднего коэффициента аппроксимации (Ā);
критерия Фишера;
коэффициента детерминации (R2).
Для оценки адекватности регрессионной модели на основе среднего коэффициента аппроксимации используют следующее выражение (среднюю относительную погрешность):
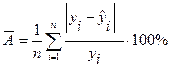 . (2.10)
. (2.10)
По своей сущности выражение (2.10) представляет собой относительную погрешность между реальными значениями результативного признака (yi) и соответствующими теоретическими значениями ( 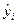 ), полученными на основе выбранной формы регрессионной модели. Уравнение регрессии считается адекватным (точным, статистически значимым), если значение среднего коэффициента аппроксимации не превышает 8…10%.
), полученными на основе выбранной формы регрессионной модели. Уравнение регрессии считается адекватным (точным, статистически значимым), если значение среднего коэффициента аппроксимации не превышает 8…10%.
Наиболее полно и точно проверка адекватности регрессионных моделей проводится с помощью критерия Фишера:
если Fрасч. > Fкр, то принимается основная гипотеза (Ho), свидетельствующая о правильности и статистической значимости выбранной формы взаимосвязи исследуемых факторов;
если Fрасч. < Fкр, то принимается альтернативная гипотеза (H1), свидетельствующая о статистической незначимости выбранной формы взаимосвязи исследуемых факторов.
Эмпирическое (расчетное) значение критерия (Fрасч.) определяется с помощью следующего выражения:
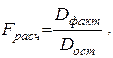 (2.11)
(2.11)
где Dфакт – дисперсия факторная (2.12);
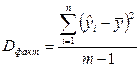 , (2.12)
, (2.12)
Dост – дисперсия остаточная, определяема по выражению (2.13);
m – число параметров уравнения регрессии;
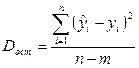 . (2.13)
. (2.13)
Табличное (критическое) значение критерия (Fкр.) определяется с помощью справочников (приложение А) или по таблицам Excel (раздел мастера функций «Статистические»):
Fкр=FРАСПОБР(α=1-P; ν1; ν2), (2.14)
где ν1 и ν2 - степенисвободы (ν1=m-1; ν2=n-m).
Сущность чисел степеней свободы (df – degrees of freedom) заключается в определении чисел свободы независимого варьирования признака, т.е указывают сколько независимых отклонений из n возможных требуется для образования данной суммы квадратов.
Следует заметить, что процесс оценки адекватности (статистической значимости) регрессионных моделей является составной частью дисперсионного анализа эконометрического исследования, поэтому довольно часто на практике процедура оценки адекватности регрессионной модели по критерию Фишера сопровождается (дополняется) построением таблицы дисперсионного анализа (таблица 2.1).
Таблица 2.1 – Вариант построения таблицы дисперсионного анализа
| Число степеней свободы(df) | Сумма квадратов(SS) | Оценка дисперсии(MS) | Расчетное значение критерия Фишера(F) | Табличное значение критерия Фишера(F) | |
| Регрессия | m-1 | (RSS) | Dфакт = RSS/(m-1) | Fрасч | Fтабл |
| Остаток | n-m | (ESS) | Dост = ESS/(n-m) | ||
| Общая | n-1 | (TSS) | Dобщ = TSS/(n-1) |
Примечание: TSS = RSS + ESS
TSS (total of sum squares) – общая сумма квадратов;
RSS (regression of sum squares) – факторная сумма квадратов;
ESS (error of sum squares) – остаточная сумма квадратов.
Процедура вычисление расчетного значения критерия Фишера тесно связана с процедурой вычисления коэффициента детерминации (R2).
Сущность коэффициента детерминации заключается в том, что он показывает зависимость вариации значений результативного признака (в %) от вариации значений фактора-признака (независимой переменной).
Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Равенство коэффициента детерминации единице означает, что объясняемая переменная в точности описывается рассматриваемой моделью (наличие функциональной связи).
Иногда (при больших значениях объема выборки (n)) используют упрощенную формулу для вычисления коэффициента детерминации R2:
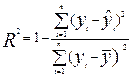 . (2.15)
. (2.15)
Недостатки применения выборочного коэффициента детерминации. Основная проблема применения (выборочного) R2 заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют. Поэтому сравнение моделей с разным количеством признаков с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели. Так, для того, чтобы была возможность сравнивать модели с разным числом признаков, обычно применяется скорректированный (нормированный) коэффициент детерминации, в котором используются несмещённые оценки дисперсий (“даёт штраф” за дополнительно включённые признаки):
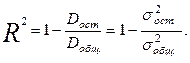 (2.16)
(2.16)
Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве признаков), поэтому интерпретировать его как долю объясняемой дисперсии уже нельзя. Тем не менее, применение показателя в сравнении вполне обоснованно. Для моделей с одинаковой зависимой переменной и одинаковым объемом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии (Dост) или стандартной ошибки модели (Dобщ).
Приведенные выше выражения для вычисления коэффициента детерминации также используют при оценке тесноты взаимосвязи факторов нелинейной регрессии.
Дата добавления: 2018-05-10; просмотров: 1517;











