Понятие о вынужденных колебаниях

Пусть на точку М, движущуюся по оси x, кроме силы 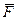, пропорциональной расстоянию x, и силы сопротивления среды 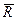, пропорциональной скорости, действует еще и периодически изменяющаяся сила 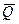(рис. 9.5), проекция которой на ось x равна

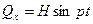. (9.20)

Силу 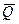называют возмущающей си­лой, а колебания, происходящие под дей­ствием этой силы, называют вынужден­ными. Величина р в равенстве (9.20) является частотой возмущающей силы.

Дифференциальное уравнение движения точки М имеет вид:

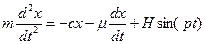. (9.21)

Разделив обе части этого уравнения на m и обозначив 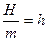, приведем уравнение (9.21) к виду:

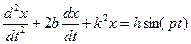. (9.22)

Это есть линейное дифференциальное уравнение второго порядка с постоянными коэффициентами и с правой частью отличной от нуля. Общее решение этого уравнения можно представить в виде:

,

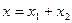где x₁ – общее решение уравнения (9.22), но без правой части, то есть при b< k это решение имеет вид (9.17), а x₂ – какое-либо частное решение данного уравнения. Решение x₂ ищут в виде:

.

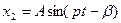Тогда, общее решение дифференциального уравнения, дающего закон движения материальной точки при наличии возмущающей силы, будет иметь вид:

, (9.23)

где а и a являются постоянными интегрирования и определяются по начальным условиям, а значения А и b определяются по формулам:

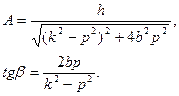(9.24)

Из анализа уравнений (9.24) следует, что наибольшего значения амплитуда вынужденных колебаний достигает при p=k, то есть в том случае, когда частота вынужденных колебаний равна частоте свободных колебаний точки, совершаемых под действием только восстанавливающей силы. Этот случай совпадения частот вынужденных и свободных колебаний носит название резонанса. Явление резонанса характерно тем, что в этом случае амплитуда колебаний точки достигает значения, близкого к максимальному.

Обозначим 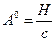- статическое смещение материальной точки под действием постоянной силы. Тогда h - коэффициент динамичности можно определить из выражения:

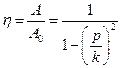. (9.25)

Вынужденные колебания обладают следующими важными свойствами, отличающими их от собственных колебаний точки:

1. Амплитуда вынужденных колебаний от начальных условий не зависит.

2. Вынужденные колебания при наличии сопротивления не затухают.

3. Частота вынужденных колебаний равна частоте возмущающей силы и от характеристик колеблющейся системы не зависит, то есть возмущающая сила «навязывает» системе свою частоту колебаний.

4. Даже при малой возмущающей силе можно получить интенсивные вынужденные колебания, если сопротивление мало, а частота p близка к k (резонанс).

5. Даже при больших значениях возмущающей силы вынужденные колебания можно сделать сколь угодно малыми, если частота p будет много меньше k.

Список использованной литературы:

1. Воронков И.М. Курс теоретической механики. Изд-во «Наука», М., 1965.

2. Краткий курс теоретической механики. Тарг С.М., Главная редакция физико-математической литературы изд-ва «Наука», 1970.

3. Чернилевский Д.В., Лаврова Е.В., Романов В.А. Техническая механика. – М.: Наука. Главная редакция физико-математической литературы, 1982.