Кинетическая энергия материального тела в различных видах движения
Материальное тело есть совокупность отдельных материальных точек. Кинетическая энергия тела, совершающего поступательное движение равна половине произведения массы тела на квадрат скорости его центра масс:
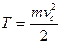 .
.
Центром масс системы называется точка С, координаты которой находятся по формулам:
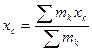 ,
, 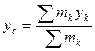 ,
, 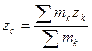 . (8.8)
. (8.8)
Пусть тело вращается вокруг неподвижной оси z с угловой скоростью w (рис. 8.2). При вращении тела абсолютная величина скорости любой точки тела равна 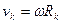 , тогда кинетическая энергия равна:
, тогда кинетическая энергия равна:
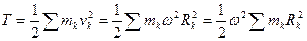 .
.
Величина, равная сумме произведений массы каждой точки на квадрат расстояния от оси вращения, называется моментом инерции Iz тела относительно оси z. Iz – мера инерции тела во вращательном движении:
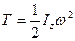 . (8.9)
. (8.9)
Осевой момент инерции можно представить в виде:
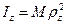 , (8.10)
, (8.10)
где rz – радиус инерции тела относительно оси Оz, М – масса тела.
Теорема Кенига. Кинетическая энергия тела, совершающего плоскопараллельное движение, равна сумме кинетических энергий поступательного движения тела со скоростью центра масс и вращательного движения вокруг оси, проходящей через центр масс:
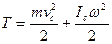 . (8.11)
. (8.11)
 Момент инерции Iz твердого тела относительно какой-либо оси z равен моменту инерции Iс этого тела относительно оси, проходящей через центр масс тела и параллельной оси z, сложенному с произведением массы тела на квадрат расстояния между осями d
Момент инерции Iz твердого тела относительно какой-либо оси z равен моменту инерции Iс этого тела относительно оси, проходящей через центр масс тела и параллельной оси z, сложенному с произведением массы тела на квадрат расстояния между осями d
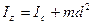 . (8.12)
. (8.12)
Дата добавления: 2018-05-10; просмотров: 916;











