Моменты инерции некоторых простых однородных тел

1. Кольцо. Окружность. Вычислим момент инерции материальной окружности радиуса R и массы М относительно ее центра О (рис. 8.3). Для этого разобьем всю окружность на бесконечно малые элементы массой m. Все элементы находятся от точки О на одном расстоянии R, поэтому искомый момент равен:

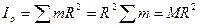. (8.13)

2. Тонкий диск. Момент инерции диска радиуса R и массы М относительно его центра О (рис. 8.4) вычислим следующим образом. Разобьем диск концентрическими окружностями на элементарные плоские кольца радиуса r, шириной - Dr. Массу кольца обозначим m. Искомый момент инерции равен сумме всех моментов инерции элементарных колец:

.

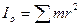Обозначим поверхностную плотность через g, тогда

.

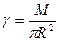Площадь элементарного кольца представим в виде:

,

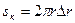тогда

.

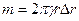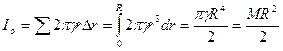. (8.14)

3. Круглый цилиндр радиуса R, массой М. Разобьем весь цилиндр на тонкие диски. Момент инерции диска

,

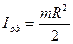где m – масса диска.

Искомый момент инерции цилиндра равен сумме моментов инерции всех дисков

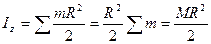. (8.15)

4. Шар. Вычислим момент инерции шара массой М и радиусом R относительно его центра. Обозначим плотность, приходящуюся на единицу объема r.

,

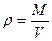где V – объем шара.

,

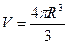тогда

.

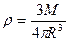Разобьем шар концентрическими сферами на бесконечно тонкие сферические слои радиуса r и толщиной Dr. Так как все частицы слоя находятся на одинаковом расстоянии от центра О, то момент инерции слоя равен

.

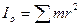Объем сферы равен:

,

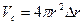масса сферы:

,

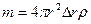тогда момент инерции шара равен:

.

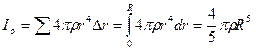Подставляя значение r, получим:

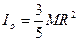. (8.16)