Свободные колебания без учета сил сопротивления

Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы 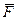, направленной к неподвижному центру Ои пропорциональной расстоянию от этого центра. Проекция силы 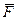на ось Оx (рис. 9.1) будет равна:

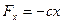. (9.1)

Дифференциальное уравнение движения точки М имеет следующий вид:

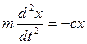, (9.2)

где с – коэффициент жесткости пружины [H/м], он показывает, какую силу необходимо приложить к пружине, чтобы растянуть или сжать её на единицу длины.

Разделив это уравнение на m и вводя обозначение 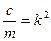, приведем его к виду:

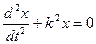. (9.3)

Уравнение (9.3) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка ищут в виде: 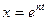. Пологая в уравнении (9.3) 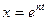, получим для описания n так называемое характеристическое уравнение, имеющее вид: 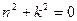. Так как корни этого характеристического уравнения являются чисто мнимыми (n_1,2=±ik),то, как известно из теории дифференциальных уравнений, общее решение уравнения (9.3) имеет вид:

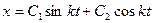, (9.4)

где С₁ и С₂ – постоянные интегрирования.

Если вместо постоянных С₁ и С₂ ввести постоянные а и a, такие, что , , то получим:

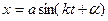. (9.5)

Уравнение (9.5) есть уравнение гармонического колебания. То есть, в случае прямолинейного движения под действием восстанавливающей силы, пропорциональной расстоянию от центра, материальная точка совершает гармоническое колебание.

Величина а – наибольшее отклонение точки М от центра О,называется амплитудой колебания, аргумент 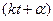называется фазой колебания, а величина a называется начальной фазой колебания.

Скорость точки при гармоническом колебании определяется по формуле:

. (9.6)

Промежуток времени Т, в течение которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза изменяется на 2p, следовательно kT=2p, откуда период

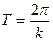. (9.7)

Величина n, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний:

. (9.8)

Величина k отличается от n только постоянным множителем 2p, то есть эта величина определяет число полных колебаний, которые совершает точка в течение 2p секунд. Эта величина k называется круговой частотой колебания.

Значения а и a - определяются по начальным условиям движения. Считая при t=0 x=0 и v=v₀, получим из (9.5) и (9.6) , , 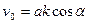отсюда находим:

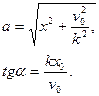(9.9)

Итак, свободные колебания при отсутствии сопротивления обладают следующими свойствами:

1. амплитуда и начальная фаза колебаний зависят от начальных условий;

2. круговая частота k, а следовательно, и период T колебаний от начальных условий не зависят и являются неизменными характеристиками данной колеблющейся системы.