Потенциальная энергия

Часть (ограниченная или неограниченная) пространства, в каждой точке которого на находящуюся там материальную точку действует некоторая сила, зависящая только от положения этой точки, то есть ее координат x, y, z, называется силовым полем. Проекции X, Y, Z силы поля на координатные оси являются некоторыми однозначными и непрерывными функциями от x, y, z. То есть 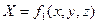, , 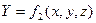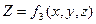. Допустим, что существует такая функция координат U(x, y, z), частные производные которой по координатам равны проекциям силы поля на соответствующие координатные оси

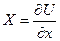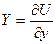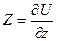, , . (8.3)

Такая функция U называется силовой функцией данного силового поля, а силовое поле в этом случае называется потенциальным. Найдем выражение элементарной работы силы потенциального поля:

,

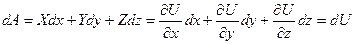то есть элементарная работа силы потенциального поля равна полному дифференциалу силовой функции.

Следовательно, работа на конечном пути, когда точка приложения силы перемещается из положения М₀ в положение М, выразится так:

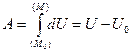, (8.4)

то есть работа силы потенциального поля равна разности значений силовой функции в конечной и начальной точках пути и, следовательно, не зависит ни от вида, ни от длины траектории, по которой перемещается точка приложения силы из положения М₀ в положение М.

Отсюда следует, что в случае однозначной силовой функции U работа силы потенциального поля на всякой замкнутой траектории равна нулю.

Пусть точка М₀(x₀, y₀, z₀) будет какая-либо произвольно выбранная неподвижная (нулевая) точка, в которой силовая функция имеет значение U(x₀, y₀, z₀).

Работа, производимая силой при перемещении материальной точки из положения М в «нулевую точку» М₀, называется потенциальной энергией в точке М.

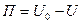. (8.5)

Очевидно, что в нулевой точке М₀ потенциальная энергия равна нулю.