Принцип Даламбера. Силы инерции

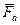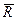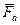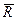Пусть материальная точка М массы m, на которую наложены некоторые связи, совершает движение, вызываемое приложенной к ней активной силой . Освободим точку от связей и заменим их действие реакциями ; сложив силы и , получим силу :

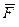, (6.5)

под действием которой теперь уже свободная точка совершает движение (рис.6.1).

Рис. 6.1

На основании второго закона Ньютона:

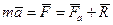. (6.6)

Введем обозначение 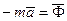, тогда

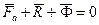. (6.7)

Вектор , направленный в сторону противоположную ускорению точки, и по модулю равный произведению массы точки на модуль ее ускорения, называ­ется силой инерции материальной точки.

Принцип Даламбера. Если к действующим на точку активным силам и ре­акциям связей добавить силу инерции, мысленно приложенную к точке, то в каждый момент времени полученная система сил будет уравновешенной. Принцип Даламбера представляет собой формальный математический прием, удобный для решения задач динамики, так как позволяет динамические урав­нения движения записывать в форме уравнений равновесия.

Работа

В качестве характеристики действия силы на материальную точку (или тело) можно рассматривать работу силы. Работа – это мера действия силы по отношению к расстоянию, пройденному точкой ее приложения. Точка прило­жения постоянной силы 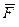движется по прямой, совпадающей с линией дейст­вия силы. Работа этой силы равна произведению ее модуля F на длину пути s, пройденного точкой приложения силы, взятому со знаком «+» или «-».

. (6.8)

Знак «+» берется в случае, когда направления силы и перемещения совпа­дают, знак «-» - когда эти направления противоположны.

Размерность единицы работы в Международной системе единиц (СИ) – джоуль (Дж). Один джоуль – это работа, совершаемая силой в один ньютон на прямолинейном участке пути длиной один метр.

При этом считается, что линия действия силы совпадает с прямой, по кото­рой движется точка ее приложения.

Если точка приложения силы также перемещается по прямой, совпадающей с линией действия силы, но модуль силы F есть величина переменная, завися­щая от точки приложения силы, то для того, чтобы найти работу переменной силы на отрезке пути длиной l, разобьем этот отрезок на достаточно большое число n малых участков Ds₁, Ds₂ ,... Ds_n. Тогда можно считать, что в пределах Ds_i модуль силы постоянен и равен некоторому своему значению F_i в какой-либо точке отрезка. Элементарную работу силы F найдем по формуле:

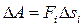. (6.9)

Вычисляя сумму элементарных работ и переходя к пределу, найдем работу переменной силы F на прямолинейном участке:

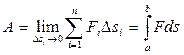. (6.10)

Для того чтобы взять этот интеграл, модуль силы следует выразить как функцию переменной s: F=f(s).