Представление синусоидальных величин комплексными числами.
Для того чтобы представить заданную в тригонометрической форме синусоидальную величину
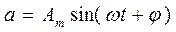
с начальной фазой j комплексным числом, проведем на комплексной плоскости из начала координат под углом j к оси действительных величин вектор, длина которого в масштабе построения равна амплитуде Am исходной синусоидальной величины.
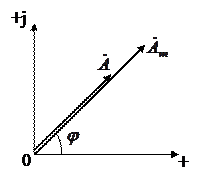
Конец этого вектора находится в точке, которой соответствует определенное комплексное число - комплексная амплитуда синусоидальной величины:
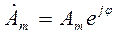
При увеличении во времени фазы (wt + j) синусоидальной величины угол между вектором и осью действительных величин растет, то есть получается вращающийся вектор
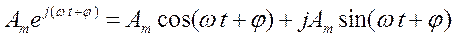 .
.
Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным действующим значением синусоидальной величины:
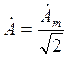 .
.
Применяется три формы записи комплексного значения синусоидальной величины:
1) показательная
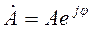 ,
,
2) тригонометрическая
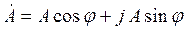 ,
,
3) алгебраическая
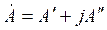 ,
,
где 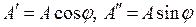 – действительная и мнимая составляющие комплексного значения синусоидальной величины;
– действительная и мнимая составляющие комплексного значения синусоидальной величины; 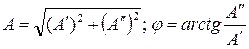 .
.
При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин. Например, синусоидальному току
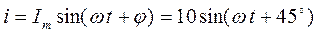
соответствует комплексное значение тока
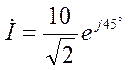 .
.
Дата добавления: 2018-05-10; просмотров: 1692;











