Условие передачи максимальной мощности приемнику
В устройствах связи, в электронике, автоматике и т. п. очень часто желательно передать от источника к приемнику наибольшую возможную в данных условиях энергию, причем КПД передачи имеет второстепенное значение.
В качестве простого примера рассмотрим питание приемника с сопротивлением rн от источника энергии с ЭДС Е и внутренним сопротивлением rвн, находящегося на некотором расстоянии от приемника и соединенного с приемником двухпроводной линией с общим сопротивлением проводов rп.
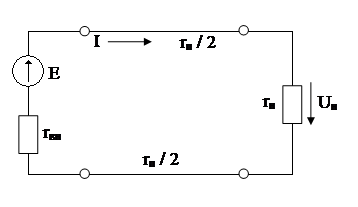
Обозначим сумму внутреннего сопротивления rвн источника энергии и сопротивления проводов rп через r, то есть r = rп + rвн. По закону Ома ток в этой цепи равен:
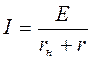 .
.
и мощность приемника (по закону Джоуля - Ленца) равна:
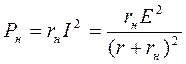 .
.
При двух предельных значениях сопротивления rн = 0 и rн = ¥ мощность приемника равна нулю, так как в первом случае равно нулю напряжение между выводами приемника, а во втором случае – ток в цепи. Следовательно, некоторому определенному значению rн соответствует наибольшее возможное (при данных E и r) значение мощности приемника. Чтобы определить это значение сопротивления rн, приравняем нулю первую производную от мощности Pн по rн:
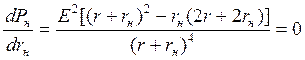 .
.
Так как знаменатель этого выражения не равен бесконечности и Е ¹ 0, то
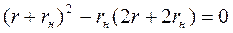 .
.
Отсюда следует, что мощность приемника будет максимальна при условии
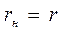 .
.
Эта максимальная мощность равна:
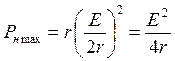 .
.
Это равенство называют условием максимальной мощности приемника.
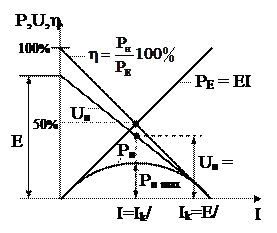
На рисунке показаны зависимости от тока мощности приемника
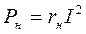 ,
,
мощности источника ЭДС
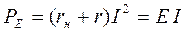
и КПД передачи энергии
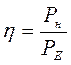 .
.
Дата добавления: 2018-05-10; просмотров: 2140;











