Меры сходства и различия нечетких категорий

Принятие решений в условиях неполной и неоднозначной информации об объекте исследования приводит к слабоформализованным задачам, описываемым нечеткими условиями и признаками. Степень достоверности полученных решений зависит от требований, предъявляемых к используемым методам и моделям их исследования. В задачах сравнения объектов, признаков, задаваемых функциями принадлежностей, нечеткость может быть формализована различными способами. Существуют следующие основные классификационные признаки способов формализации нечеткости: по виду представления нечеткой субъективной оценки какой-либо величины (нечеткого множества); по виду области значений функции принадлежности (ФП); по виду области определения ФП; по виду соответствия между областью определения и областью значений (однозначное, многозначное); по признаку однородности или неоднородности области значений ФП.

Обзор различных способов формализации нечеткости показал, что в этом направлении развиваются два основных подхода. Первый базируется на обобщении понятия принадлежности элемента множеству, приводящему к размыванию границ множества, а в предельном случае к появлению объекта с неопределенными границами – полумножества. Второй подход предполагает описание нечеткости с помощью классов нечетких множеств, для формирования которых используются меры сходства и различия. В настоящее время существует достаточно методов, позволяющих определить меру сходства (различия) между двумя нечеткими множествами.

Сходство и различие объектов определяется мерами близости (удаления), а признаков - мерами связи.

Количественное определение тесноты связи между признаками предполагает определение меры соответствия вариации результирующего признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных признаков. Мера связи двух признаков А₁ и А₂, рассматриваемых на множестве объектов Х и задаваемых функциями принадлежностей А₁={<m_A1(x_i) / x_i>} и А₂={<m_A2(x_i) / x_i>}, где 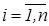, определяется с использованием статистических показателей. Выбор статистических показателей определяется законом распределения параметров или случайной величины. Параметрические методы определения тесноты связи применимы, если сделаны предположения относительно параметров распределения величин (например, в случае нормального закона – относительно математического ожидания и дисперсии). Использование непараметрических методов определяется распределением случайной величины (подчинение закону Бернулли, Пуассона, нормальному и т.д.).

Сделаем предположение о наличии нормального закона распределения рассматриваемых величин, в этом случае для расчета меры связи двух признаков используются параметрические методы, применение которых рассмотрим на примере расчета коэффициента корреляции Пирсона r Î[0,1] , вычисляемого по формуле (2.24):

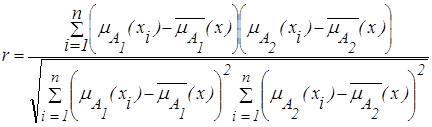
(2.24)

Если r = 0, то признаки А₁ и А₂ являются независимыми, если r = 1 - признаки являются зависимыми. В случае если не возможно однозначно оценить силу связи между признаками, значимость коэффициента корреляции проверяется на основе критерия Стьюдента следующим образом:

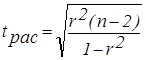
Расчетное значение сравнивается с табличным значением t_q,n=n-2, где q– уровень значимости, n – количество степеней свободы. Если расчетное значение больше табличного, это свидетельствует о значимости коэффициента корреляции, а, соответственно, высокой силе связи между признаками.

Пример 2.8. Оценим меру связи двух признаков «молодой» и «энергичный» на множестве сотрудников отдела организации Х={x₁, x₂, x₃, x₄, x₅} в возрасте от 20 до 40 лет. Нечеткие множества А₁ и А₂, соответствующее нечетким понятиям (признакам) «молодой» и «энергичный» могут быть представлены функциями принадлежностей:

A₁={<x₁/0,5>, <x₂/0,6>, <x₃/1>, <x₄/0,8>, <x₅/0,4>},

A₂={<x₁/0,3>, <x₂/0,35>, <x₃/0,6>, <x₄/0,8>, <x₅/0,5>}.

По формуле (2.24) рассчитаем меру связи двух признаков:

.

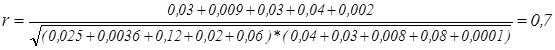Мера связи между признаками достаточно высокая, т.е. энергичность людей зависит от возраста.

В общем случае, мера связи на множестве объектов х_iÎХ, рассматриваемых относительно нечетких понятий (признаков) А₁, А₂,…, А_р и определяемых функциями принадлежностей А_j={<m_Aj(x_i) / x_i>}, представляет собой двухмерную симметричную квадратную матрицу R:

	r11,	…,	r1p
R =	r21,	…,	r2p
…	…	…
	rp1,	…,	rpp

где r_ij - мера связи между признаками A_i и A_j.

Заключение о наличии связи между переменными делается в том случае, когда увеличение значения одной переменной сопровождается устойчивым увеличением или уменьшением значений другой. Меры связи вычисляются по формуле (2.25).

,

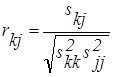(2.25)

где 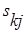определяется по формуле (2.24), , .

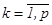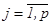Сила связи рассматриваемой совокупности изменяется в пределах от 0 до 1. В случае если не возможно однозначно оценить силу связи между признаками, проверка значимости коэффициента корреляции осуществляется по критерию Фишера:

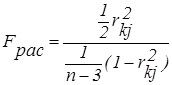
Связь между признаками можно считать сильной, если .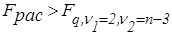

Среди непараметрических методов для оценки тесноты связи можно использовать следующие:

- коэффициент ранговой корреляции Спирмана;

- ранговый коэффициент Кэндела;

- множественный коэффициент ранговой корреляции – коэффициент конкордации и т.д.

Для количественной оценки сходства объектов используется понятие метрики. Сходство и различие между объектами устанавливается в зависимости от метрического расстояния d(x_i, x_j) между ними. Для анализа метрического расстояния между объектами используются меры близости и удаленности, к которым предъявляется требование эквивалентности нечеткого отношения, определяющее согласованность рассуждений эксперта. Эквивалентность нечеткого отношения определяется выполнением условий (свойств нечетких отношений, приведенных в п.2.3): симметричности, транзитивности и неотрицательности d(x_i, x_j)≥0, где i¹j, а так же для меры близости - условием рефлексивности, для меры удаленности - антирефелексивности.

Рассмотрим три нечетких подмножества A, B, CÌ X (cardX=n):

A={(x₁/a₁), (x₂/a₂), …, (x_n/a_n)},

B={(x₁/b₁), (x₂/b₂), …, (x_n/b_n)},

C={(x₁/c₁), (x₂/c₂), …, (x_n/c_n)}.

Предположим, что мы определим расстояние D(a_i, b_i) между a и b для всех i и определим расстояния D(a_i, с_i), D(b_i, c_i). Тогда выполняется:

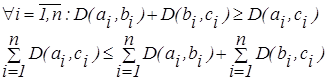
	(2.26)
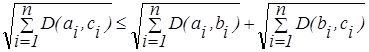
	(2.27)

Формулы (2.26), (2.27) дают две оценки расстояния между нечеткими множествами:

- линейная оценка, используется для определения различий между объектами, описываемыми количественными признаками, и интерпретируется как число несовпадений значений признаков у рассматриваемых объектов;

- квадратичная оценка, используемая для определения меры сходства между объектами, описываемыми как качественными, так и количественными признаками и применяемая для придания больших весов более отдаленным друг от друга объектам.

Обобщенное расстояние Хемминга или линейное расстояние определятся следующим образом:

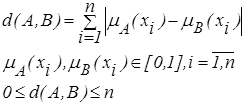
(2.28)

Обобщенное относительное расстояние Хемминга определяется:

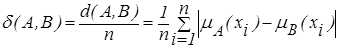
(2.29)

Евклидово или квадратичное расстояние определятся:

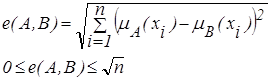
(2.30)

Относительное Евклидово расстояние определяется:

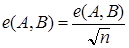
(2.31)

Пример 2.9. Определить меры сходства и различия нечетких множеств, заданных функциями принадлежностей:

A={(x₁ /0), (x₂ /0,3), (x₃ /0,7), (x₄ /1), (x₅ /0), (x₆ /0,2), (x₇ /0,6)};

B={(x₁ /0,3), (x₂ /1), (x₃ /0,5), (x₄ /0,8), (x₅ /1), (x₆ /0,5), (x₇ /0,6)}.

С помощью формулы (2.29) определим меру различия между объектами:

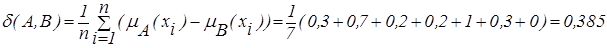С помощью формулы (2.31) определим меру сходства между объектами:

.

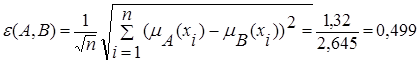Сравнивая полученные метрик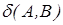и и 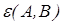можно отметить, что мера различия между нечеткими объектами доминирует над мерой сходства нечетких объектов.

В общем случае меры близости (удаленности) множества объектов Х₁,Х₂,…,Х_Р определяемых множеством признаков А={a_i}, и задаваемых функциями принадлежностей X_i={<m_Xi(a_i)/a_i>} представляют собой квадратную симметричную матрицу D:

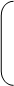
	d11,	…,	d1Р
D=	d21,	…,	d2P
…	…	…
	dP1,	…,	dPP

где d_ij - значения меры близости (удаленности) между объектами Х_i и X_j, определяемые по формулам (2.28) и (2.30).

Все рассматриваемые метрики, используемые для сравнения объектов (признаков), задаваемых нечеткими категориями, также применимы для количественной оценки сходства нечетких и обычных (четких) множеств. Необходимость их оценки обусловлена внутренней неопределенностью, двусмысленностью объекта х в отношении обладания им свойством K (порождающим нечеткое множество А). Неопределенность выражается принадлежностью объекта одновременно двум противоположным классам: классу объектов, «обладающих свойством K», и классу объектов, «не обладающих свойством K». Эта двусмысленность максимальна, когда степени принадлежности объекта обоим классам равны, т.е. m_A(x)= 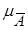(x)=0,5, и минимальна, когда объект принадлежит только одному классу, т.е. либо m_A(x) = 1 и 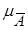(x)=0, либо m_A(x) = 0 и 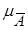(x)=1.

Для определения мер различия (сходства) между нечеткими и обычными множествами, рассмотрим понятие обычного (четкого) множества. Обозначим через 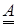- ближайшее четкое множество, находящееся на наименьшем расстоянии от нечеткого множества А, определяемое подмножеством с характеристической функцией:

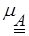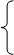
=		0, если mA(xi) £ 0,5	(2.32)
1, если mA(xi) > 0,5

На рис.2.13 приведен пример построения обычной функции принадлежности, ближайшей к нечеткой.

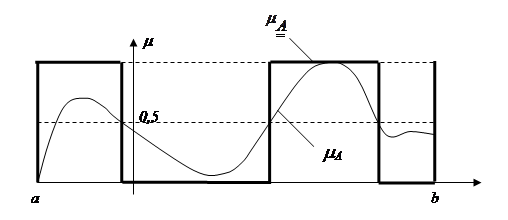Рис. 2.13. Функция принадлежности, ближайшая к нечеткой

Мера различия нечеткого и обычного множеств называется показателем размытости нечеткого множества и определяется через индекс нечеткости.

Существует ряд методов расчета, обратимся к некоторым из них.

Первый метод расчета индекса нечеткости опирается на понятие расстояния между нечеткими множествами.

Линейный индекс нечеткости определяется по свойствам обобщенного расстояния Хемминга:

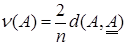
(2.33)

Квадратный индекс нечеткости определяется по средствам обобщенного евклидова расстояния:

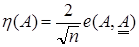
(2.34)

Рассмотренные линейный и квадратичный индексы нечеткости, используя понятие расстояния и понятие обычного множества, ближайшего к нечеткому, можно определить, используя операцию дополнения, следующим образом:

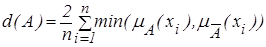- линейный индекс,

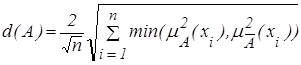- квадратичный индекс.

Пример 2.10. Для нечетких множеств, заданных в примере 2.9, определить индекс нечеткости по средствам обобщенного евклидова расстояния и расстояния Хемминга.

С помощью формулы (2.33) определим линейные индексы нечеткости для нечетких множеств A, B, :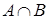

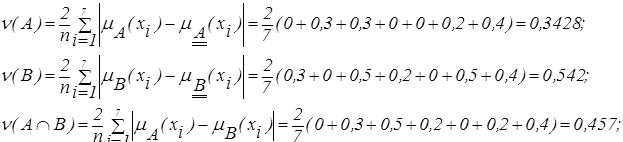С помощью формулы (2.34) определим квадратный индекс нечеткости нечеткого множества А:

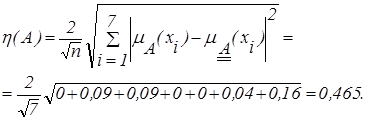
Существует другой способ определения нечеткости, представленный методом расчета нечеткости через энтропию.

Энтропия системы с n состояниями e₁,e₂, ..., e_n, с которыми связаны вероятности p₁,p₂, ..., p_n определяется выражением:

,

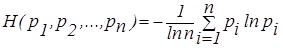где 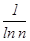- нормировочный коэффициент, позволяющий осуществить оценку энтропии в интервале H Î [0,1].

В случае нечетких множеств осуществим нормирование нечеткого множества по величине С(А), называемой мощностью нечеткого множества и определяемой:

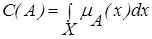в случае XÌ R;

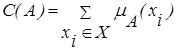для конечного универсального множества.

Степень принадлежности нормированного нечеткого множества определяется, как: .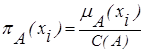

Общую формулу, позволяющую подсчитать энтропию по нечеткости, можно записать в следующем виде:

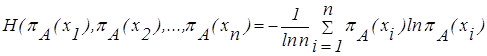
(2.35)

Метод подсчета нечеткости через энтропию зависит не от собственно значений функции принадлежности, а от их относительного значения.

Приведенные меры близости (удаленности) объектов и меры размытости нечетких множеств являются основой формирования групп схожих между собой объектов (кластеров), построения которых является целью кластерного анализа. Необходимость развития методов кластерного анализа и их использования продиктована, прежде всего, тем, что они помогают построить научно обоснованные классификации, выявить внутренние связи внутри совокупности, осуществить поиск существующей структуры в изучаемой совокупности объектов. Существующие методы кластеризации можно классифицировать на четкие и нечеткие. Нечеткие методы позволяют одному и тому же объекту принадлежать одновременно нескольким кластерам, но с различной степенью. Нечеткая кластеризация во многих случаях более «естественна», чем четкая, например, для объектов, расположенных на границе классов.

Нечеткая кластеризация представляет собой метод разбиения множества разбросанных данных, задаваемых функциями принадлежностей на несколько групп. Разбиение осуществляется так, чтобы данные в одной группе обладали похожими признаками, а признаки в среднем между группами максимально различались.

Пусть исследуемая совокупность представляет собой конечное множество элементов 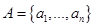, которое получило название множество объектов кластеризации. В рассмотрение также вводиться конечное множество признаков или атрибутов 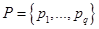, каждый из которых количественно представляет некоторое свойство или характеристику элементов рассматриваемой проблемной области. При этом 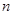- общее количество объектов данных, а 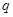- общее количество измеримых признаков.

Далее предполагается, что для каждого из объектов кластеризации некоторым образом измерены все признаки множества 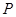в некоторой количественной шкале. Тем самым, каждому из элементов 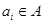поставлен в соответствие некоторый вектор 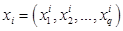, где 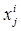- количественное значение признака 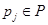для объекта 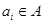. Векторы значений признаков 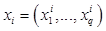удобно представлять в виде матрицы данных 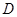размерности 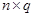каждая строка, которой равна значению вектора .

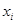Задача нечеткого кластерного анализа формулируется следующим образом: на основе исходных данных 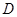определить такое нечеткое разбиение 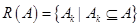множества 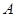на заданное число 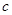нечетких кластеров 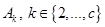, которое доставляет экстремум некоторой целевой функции 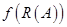среди всех нечетких разбиений.

Для решения задача нечеткого кластерного анализа требуется дополнительно уточнить вид целевой функции и тип искомых нечетких кластеров (поиск нечеткого разбиения).

Для уточнения вида целевой функции 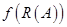, прежде всего, предполагается, что искомые нечеткие кластеры представляют собой нечеткие множества 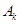, образующие нечеткое разбиение исходного множества объектов кластеризации, для которых условие 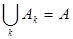принимает следующий вид:

,

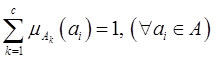
(2.36)

где 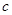- общее количество нечетких кластеров 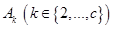, которое считается предварительно заданным.

Каждый нечеткий кластер характеризуется центрами 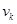искомых нечетких кластеров 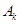, которые рассчитываются для каждого из нечетких кластеров и по каждому из признаков по следующей формуле.

,

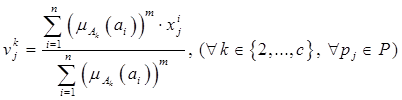
(2.37)

где 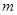- некоторый параметр, называемый экспоненциальным весом и равный некоторому действительному числу 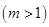. Каждый из центров кластеров представляет собой вектор 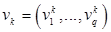в некотором 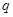- мерном нормированном пространстве.

В качестве целевой функции рассматривается сумма квадратов взвешенных отклонений координат объектов кластеризации от центров искомых нечетких кластеров:

,

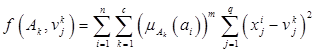
(2.38)

где 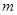- экспоненциальный вес нечеткой кластеризации, значение которого задается в зависимости от мощности множества 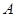. Чем больше в 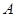элементов, тем меньшее значение выбирается для .

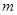Задача нечеткой кластеризации формулируется следующим образом.

Для заданных матрицы данных 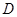, количества кластеров 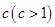, параметра 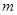определить матрицу 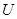значений функции принадлежности объектов кластеризации 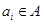нечетким кластерам 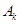, которые доставляют минимум целевой функции (2.38) и удовлетворяют ограничениям (2.36) и (2.37), а так же дополнительным ограничениям:

,

.

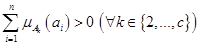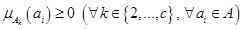Условие 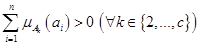исключает появление пустых кластеров в искомой нечеткой кластеризации.

Достоинством такой постановки задачи нечеткой кластеризации является естественная интерпретация, как искомых нечетких кластеров, так и их типичных представителей или центров.

Недостатком поставленной задачи является необходимость априорного задания общего числа нечетких кластеров 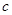, которое не всегда известно.

Алгоритм решения задачи нечеткой кластеризации методом нечетких 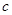-средних.