Знакопеременные ряды

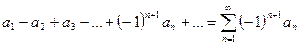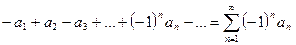Определение. Знакочередующимся рядомназывается ряд, в котором любые два соседних члена имеют разные знаки, таким образом, знакочередующийся ряд это ряд вида: или , где , .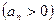

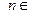Признак Лейбница

Если для знакочередующегося ряда выполняются условия:

1. 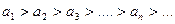(абсолютные величины членов ряда монотонно убывают)

2. 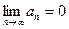, то ряд 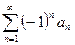сходится.

Определение. Ряд, содержащий и положительные и отрицательные члены, называется знакопеременным. Всякий знакочередующийся ряд является знакопеременным.

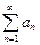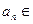Теорема.Пусть дан знакопеременный ряд , где  или 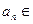. Если ряд 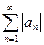, составленный из абсолютных величин его членов сходится, то и данный ряд 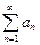также сходится. В этом случае знакопеременный ряд 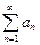называется абсолютно сходящимся. Если знакопеременный ряд 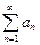сходится, а ряд 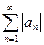расходится, то данный ряд 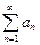называется условно сходящимся

Для ответа на вопрос о сходимости ряда 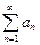можно применить все признаки, используемые для исследования рядов с положительными членами.

Пример. Исследовать на сходимость ряд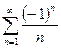

Решение.

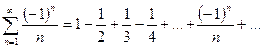
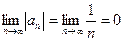, т.к. ряд 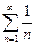- расходится, то ряд 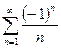- условно сходящийся ряд.

Пример. Исследовать на сходимость ряд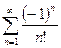

Решение.

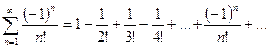
Составим ряд из абсолютных величин членов данного ряда: ,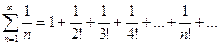

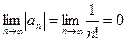
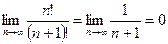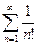Применяя признак Даламбера, получим , ряд сходится, следовательно, ряд 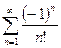абсолютно сходящийся.