Нечеткие отношения и отображения на нечетких множествах
При описании суждений не менее важное место занимают нечеткие отношения на множествах. Нечетким бинарным отношением RA на множестве Х называется нечеткое подмножество прямого произведения Х ´ Х, характеризующееся функцией принадлежности mR:Х ´ Х ® [0,1]. Значение mR для конкретной пары (xi, xj )Î Х ´ Х характеризует субъективную меру или степень выполнения отношения xi RA xj.
Если множество Х конечно и невелико, нечеткое отношение RA удобно задавать в матричном виде. Матрица М(RA) представляет собой квадратичную матрицу, строки и столбцы которой помечены элементами хÎ Х, а в ячейках записаны значения rij = mR(xi, xj).
Пример 2.5.Задать нечеткое отношение RА x≈y («x приблизительно равно y»). Пусть x, yÎ{0,1,2,3}. Тогда нечеткое отношение удобно задавать матрицей вида:
| 0,5 | 0,2 | 0,1 | |||
| М(RA)= | 0,5 | 0,6 | 0,3 | ||
| 0,2 | 0,6 | 0,8 | |||
| 0,1 | 0,3 | 0,8 |
Для непрерывных множеств Х=[0,3] и Y=[0,3] нечеткое отношение можно задать следующей функцией принадлежности: 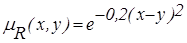 . Нечеткие отношения x≈y на дискретных и нее прерывных множествах изображены на рис. 2.10.
. Нечеткие отношения x≈y на дискретных и нее прерывных множествах изображены на рис. 2.10.
Пример 2.6.Задать нечеткое отношение RB "х намного меньше, чем y". Пусть x, yÎ{0,1,2,3}. Тогда нечеткое отношение можно задать матрицей вида:
| 0,2 | 0,6 | ||||
| М(RB)= | 0,2 | 0,6 | |||
| 0,2 | |||||
Для непрерывных множеств Х=[0,3] и Y=[0,3] нечеткое отношение "х намного меньше, чем y" можно определить такой функцией принадлежности:
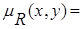
| 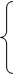
| 0, | если x ≥ y |
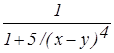 , ,
| если x < y |
Нечеткие отношения "х намного меньше, чем y" на дискретных и непрерывных множествах изображены на рис. 2.11.
Как видно из примеров, нечеткие отношения являются более гибкими по сравнению с традиционными отношениями. Они позволяют задать не только сам факт выполнения отношения, но и указывать степень его выполнения, что является очень важным для многих практических задач.
Нечеткие бинарные отношения удобно представлять в виде нечеткого графа GA = (X, LA ), где Х - множество вершин, а LA - множество нечетких дуг
LA = {< mR(xi, xj)/ (xi, xj)>}.
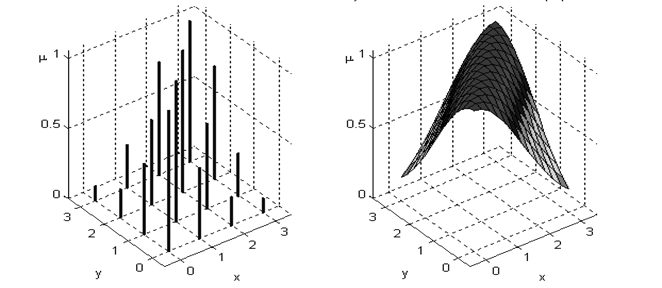
| а) нечеткое отношение на дискретных множествах | б) нечеткое отношение на непрерывных множествах |
Рис.2.10. Нечеткое отношение "х приблизительно равно y"
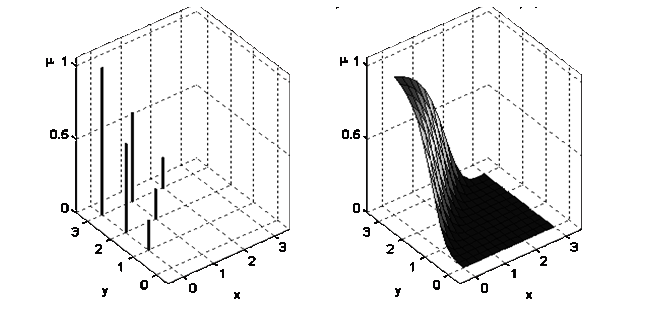
| а) нечеткое отношение на дискретных множествах | б) нечеткое отношение на непрерывных множествах |
Рис.2.11. Нечеткое отношение "х намного меньше, чем y"
Граф LA для нечеткого отношения RA, рассмотренного в примере 2.5, представлен на рис. 2.12.
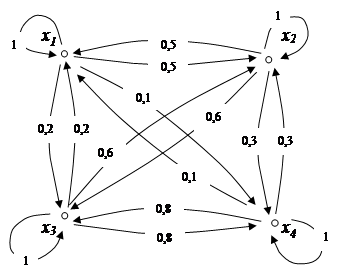
Рис.2.12. Нечеткий граф
В общем случае нечеткое n - арное отношение на множестве Х выражено декартовым произведением х1´ х2´ ... ´ хn , определенным отношениемRA с функциями принадлежности mR(х1, х2, …, хn).
Носителем нечеткого отношения RA на множествах X и Y называется подмножество декартова произведения X 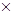 Y вида:
Y вида:
supp 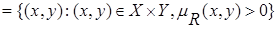 ,
,
т.е. носитель нечеткого отношения можно рассматривать как обычное отношение, связывающего все пары (x, y)Î X 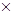 Y, для которых степень выполнения нечеткого отношения R не равна нулю. Более полезным является использование a - сечений нечеткого отношения, определения которых аналогично определениям множеств a - уровня.
Y, для которых степень выполнения нечеткого отношения R не равна нулю. Более полезным является использование a - сечений нечеткого отношения, определения которых аналогично определениям множеств a - уровня.
a - сечением нечеткого отношения R на X 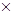 Y называется обычное отношение, связывающее все пары (x, y)Î X
Y называется обычное отношение, связывающее все пары (x, y)Î X 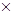 Y, для которых степень выполнения нечеткого отношения R не меньше a:
Y, для которых степень выполнения нечеткого отношения R не меньше a: 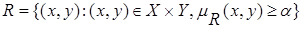 .
.
Нечеткое отношение R на X 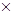 X называется рефлексивным, если для любого xÎX выполняется равенство
X называется рефлексивным, если для любого xÎX выполняется равенство 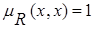 . В случае конечного множества X все элементы главной диагонали матрицы R равны 1. Примером рефлексивного нечеткого отношения может быть отношение «приблизительно равны».
. В случае конечного множества X все элементы главной диагонали матрицы R равны 1. Примером рефлексивного нечеткого отношения может быть отношение «приблизительно равны».
Нечеткое отношение R на X 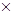 X называется антирефлексивным, если для любого xÎX выполняется равенство
X называется антирефлексивным, если для любого xÎX выполняется равенство 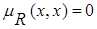 . В случае конечного множества X все элементы главной диагонали матрицы R равны 0. Примером антирефлексивного нечеткого отношения может быть отношение «значительно больше».
. В случае конечного множества X все элементы главной диагонали матрицы R равны 0. Примером антирефлексивного нечеткого отношения может быть отношение «значительно больше».
Нечеткое отношение R на X 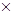 Y называется симметричным, если для любой пары (x, y)ÎX
Y называется симметричным, если для любой пары (x, y)ÎX 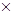 Y выполняется равенство
Y выполняется равенство 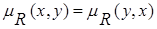 . Матрица симметричного нечеткого отношения, заданного на конечном множестве, симметричная.
. Матрица симметричного нечеткого отношения, заданного на конечном множестве, симметричная.
Нечеткое отношение R на X  Y называется асимметричным, если выражение
Y называется асимметричным, если выражение 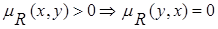 справедливо для любой пары (x, y)ÎX
справедливо для любой пары (x, y)ÎX  Y. Примером асимметричного нечеткого отношения может служить отношение «намного больше».
Y. Примером асимметричного нечеткого отношения может служить отношение «намного больше».
Нечеткое отношение R на X  X называется транзитивным, если для любой тройки (x,z)(y,z)(x,z)ÎX
X называется транзитивным, если для любой тройки (x,z)(y,z)(x,z)ÎX 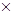 X, x,y,zÎX
X, x,y,zÎX 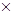 X выполняется условие
X выполняется условие 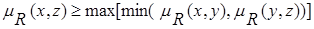 .
.
Нечеткое отношения R и R-1 на X 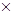 Y называется обратными, если для любой пары (x, y)ÎX
Y называется обратными, если для любой пары (x, y)ÎX  Y выполняется равенство
Y выполняется равенство 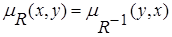 . Примером обратных нечетких отношений может служить пара «намного больше» ‑ «намного меньше».
. Примером обратных нечетких отношений может служить пара «намного больше» ‑ «намного меньше».
Пример 2.7. Определить свойства нечеткого отношения, заданного в примере 2.5.
- отношение RA рефлексивно в силу выполнения равенства 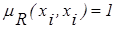 , где
, где 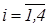 ;
;
- отношение RA симметрично в силу выполнения равенства 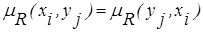 , где
, где 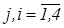 ;
;
- для оценки свойства транзитивности отношения RA необходимо проверить выполнение условия транзитивности для каждой дуги:
дуга 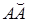 : х = x1, y = x1, x2, x3, x4, z = x1:
: х = x1, y = x1, x2, x3, x4, z = x1:
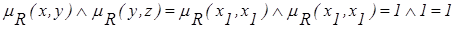 ;
;
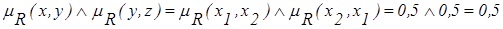 ;
;
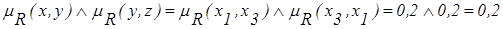 ;
;
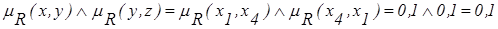 ;
;
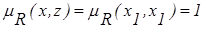 ;
; 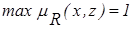 ;
; 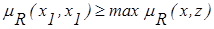 .
.
Аналогичным образом осуществляется проверка всех остальных дуг графа, представленного на рис.2.12.
Нечеткие множества, порождаемые отображениями, определяются следующим образом. Пусть f : X ®Y - отображение из X в Y , причем образ элементах обозначается через y = f(x) и пусть А - нечеткое множество в Х. Тогда отображение f порождает нечеткое множество В в Y с функцией принадлежности
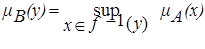 . .
| (2.19) |
Нечеткое множество В(х) в пространствеY ={y} будет условным по х, если его функция принадлежности зависит от х как от параметра. Это можно обозначить записью mB(y/x).
В результате нечеткое множество А в X порождает нечеткое множество В в Y, определенное выражением:
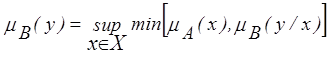
| (2.20) |
или
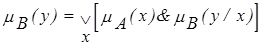 . .
| (2.21) |
Выражения (2.19) - (2.21) являются одной из формулировок принципа обобщения, играющего важную роль в теории нечетких множеств. Этот принцип позволяет расширить область определения исходного отображения fна класс нечетких множеств, а также обобщить определения операций над нечеткими множествами типа n.
Нечетким множеством типа n называется нечеткое множество, у которого значениями функции принадлежности является НМ типа n-1.Так, нечеткое множество типа 1есть a: X® [0, 1], а нечеткое множество типа 2 есть m:X ´ [0,1] ® [0, 1] и т.д.
Другими словами, нечеткое множество типа 1 полностью определяется функцией принадлежности ma(x) для всех x Î X. Для нечеткого множества типа 2 функция принадлежности mb(x) для x Î Xявляется нечетким множеством Yс функцией принадлежности fx(y),т.е.
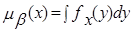
| (2.22) |
или для дискретного случая
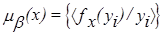 . .
| (2.23) |
Из приведенного выше становится очевидным, что нечеткость в любых проявлениях связана с функцией принадлежности, что важнейшим становится вопрос определения этой функции или ее значений (степеней принадлежности) для элементов x Î X. Этому вопросу посвящена глава 3.
Дата добавления: 2021-10-28; просмотров: 512;











