Понятие нечеткого множества
Представим произвольное непустое (универсальное) множество X = {x}. Если все элементы этого множества разложить по признакам, то получим ряд подмножеств Xi, состоящих из этих элементов и характеризующихся соответствующим i-м признаком: X1, X2,...,Xi,.... При этом, 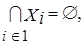 т.е. каждый элемент xjвходит только в одно подмножество. Например, если всех людей (множество X) разделить по половому признаку, то получим два подмножества: Xм и Xж. Естественно, XмÇXж=Æ, а Xм È Xж = X, где Xм Î Xм, Xж Î Xж. Теперь представим подмножества, характеризуемые возрастным признаком, например, “дети”, “подростки”, “взрослые” или, более того, “молодые” и “старые”. Подразделение людей по указанным признакам вряд ли удастся осуществить однозначно, т.е. четко. Более того, если решение этой задачи поручить различным специалистам, то вероятнее всего многие элементы множества X могут оказаться в различных подмножествах, т.е. принадлежность некоторых X не окажется однозначной, а границы между подмножествами множества X окажутся расплывчатыми, нечеткими. Такие подмножества называют нечеткими множествами.
т.е. каждый элемент xjвходит только в одно подмножество. Например, если всех людей (множество X) разделить по половому признаку, то получим два подмножества: Xм и Xж. Естественно, XмÇXж=Æ, а Xм È Xж = X, где Xм Î Xм, Xж Î Xж. Теперь представим подмножества, характеризуемые возрастным признаком, например, “дети”, “подростки”, “взрослые” или, более того, “молодые” и “старые”. Подразделение людей по указанным признакам вряд ли удастся осуществить однозначно, т.е. четко. Более того, если решение этой задачи поручить различным специалистам, то вероятнее всего многие элементы множества X могут оказаться в различных подмножествах, т.е. принадлежность некоторых X не окажется однозначной, а границы между подмножествами множества X окажутся расплывчатыми, нечеткими. Такие подмножества называют нечеткими множествами.
Нечеткое множество (подмножество А в X) определяется совокупностью упорядоченных пар, составленных из элементов x множества X и соответственных степеней принадлежности mА(xi). Степень принадлежности mА(xi) принимает значения из замкнутого интервала [0;1]. Принадлежность нечеткому множеству А может быть описана функцией mА: X® [0;1], имеющей различный характер (рис.2.1).
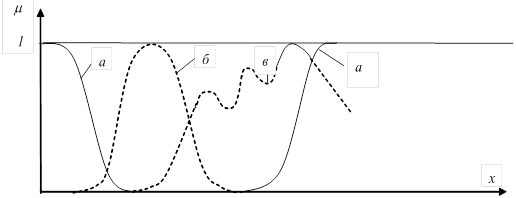
Рис.2.1. Виды функций принадлежности:
a) аммодальные; б) унимодальные; в) полимодальные
Функцией принадлежности mА(х) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента х универсального множества Х к нечеткому множеству А.
Нечеткие множества обозначаются различным образом, например:
| А = {< x, mА(x) >} |
или
| x2 | x3 | ||||
| mА(x1) | mА(x2) | mА(x3) |
Однако наиболее распространенными являются следующие формы записи:
- для конечного Х
А = {< mА(x) / x >},
- для Х, имеющего мощность континуума
| А = mА(x) / x. |
Множество Х называется областью определения функции принадлежности mА(x),или базовым множеством. В случае, когда базовое множество упорядочено (не слабее шкалы строгого порядка), Х называют базовой шкалой.
Носителем нечеткого множества А является подмножество
SA ={x | xÎX&mА(x) >0} .
Элементы, для которых mА(x) = 0, не относятся к носителям нечеткого множества А.
Если sup mА(x) = 1, то нечеткое множество называется нормальным. При sup mА(x) < 1 или sup mА(x) > 1 - нечеткое множество называется субнормальным. Нормализация субнормального множества осуществляется по формуле:
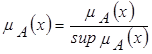 . .
|
В последующем будем иметь дело с нормальными нечеткими множествами.
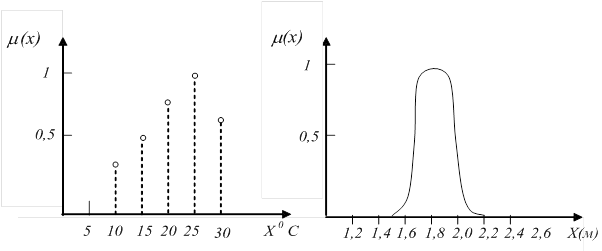
Пример 2.1. Базовая шкала Х соответствует ряду значений температуры в летний период года, расположенных в интервале от 0 до 30°С с дискретным шагом 5°. Нечеткое множество А, соответствующее нечеткому понятию “теплая погода”, может быть представлено в виде
| А= {<0/0>,<5/0>,<10/0,1>;<15/0,5>,<20/0,9>,<25/1,0>,<30/0,7>}. |
Графически данное нечеткое множество можно представить в виде отдельных точек на плоскости (рис.2.2), абсциссы которых соответствуют значениям хÎ Х, а значение ординат - функции mА(x). Носителем нечеткого множества А является конечное подмножество
SA= {10, 15, 20, 25, 30} .
Пример 2.2. На универсальном множестве Х, включающем все действительные числа, определим нечеткое множество А, соответствующее понятию “средний рост человека”. Графически это нечеткое множество можно представить кривой (рис.2.3), определяющей функцию принадлежности mА(x). Эту функцию можно также задать или определить аналитически в виде формулы, отражающей характер изменения mАв зависимости от х.
Пример 2.3. На множестве людей Х необходимо определить нечеткое множество А, соответствующее понятию “красивый человек”. Здесь очевидны два характерных момента: во-первых, функция принадлежности, а точнее, степень принадлежности каждого х будет иметь явно выраженный субъективный характер, во-вторых, как ни кстати подходит поговорка: “Все познается в сравнении”, т.е. принадлежность к А для отдельных х (и то с трудом!) можно определить лишь в сравнении, поскольку базовое множество Х не имеет количественной шкалы, т.е. не является базовой шкалой.
| ||
| Рис.2.2. Функция принадлежности нечеткого множества с дискретным носителем | Рис.2.3. Функция принадлежности нечеткого множества с непрерывным носителем |
В теории нечетких множеств существует понятие множество уровня a или a - срез нечеткого множества, через которое определяется связь с обычными теоретико-множественными представлениями.
Множеством уровня a (a - срезом) нечеткого множества А называется четкое подмножество универсального множества Х, определяемое из условия
| Хa={x Î X | mА(x)³ a}, | (2.1) |
где a выбирается из интервала значений функции принадлежности [0,1].
Пример 2.4. В примере 2.1 возьмем a = 0,7. Тогда в множество данного уровня среза войдут (четко, однозначно) те элементы х, для которых mА(x) ³ 0,7, а именно Sa ={20, 25, 30}.
Множество a - срезов образует семейство С(х) = {Хa /a Î (0,1]}, представляющее монотонную последовательность, удовлетворяющую условию
| 0 < a1£ a2£ ... £ ai £ ... £ am £ 1® ® Xa0 Ê Xa1Ê Xa2Ê ... Ê Xai Ê ... Xam Ê Xa=1 . | (2.2) |
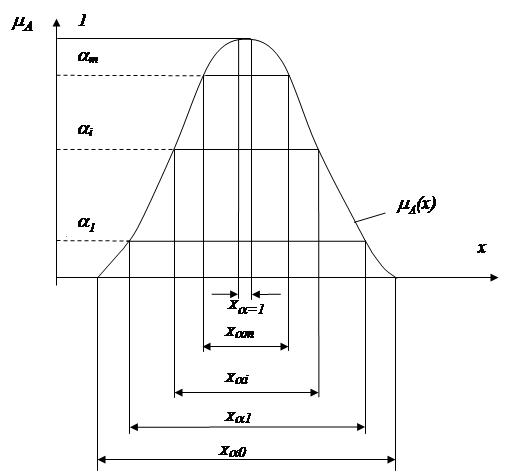
Эта последовательность иллюстрирована на рис.2.4, из которого видно, что семейство С(х) образует гистограмму. При m ® ¥ эта гистограмма превращается в функцию принадлежности mА(x). Таким образом, условие (2.2) позволяет представить нечеткое множество А с помощью четких подмножеств Xa следующим образом:
| "х, mА(x) = sup {a | xÎ Xa}. | (2.3) |
 mА
mА
mА(x)
Рис.2.4. Изображение a - срезов на плоскости mА(x)
В некоторых случаях нечеткое множество А целесообразно представлять совокупностью строгих a - срезов (множество строгого уровня a):
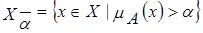 . .
| (2.4) |
Среди семейства C(х), описывающего нечеткое множество А, часто употребляются два множества:
1) множество уровня a = 1 (Xa=1), называемое ядром нечеткого множества А и обозначенное 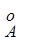 ;ядром нечеткого множества А называется четкое подмножество универсального множества Х, элементы которого имеют степени принадлежности равные единице:
;ядром нечеткого множества А называется четкое подмножество универсального множества Х, элементы которого имеют степени принадлежности равные единице: 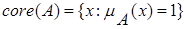 . Ядро субнормального нечеткого множества пустое.
. Ядро субнормального нечеткого множества пустое.
2) множество строгого уровня a = 0 (Xa=0), называемое носителем нечеткого множества А: Хa=0 = SA ={ xÎ X | mА(x) >0}, представленное выше.
Дата добавления: 2021-10-28; просмотров: 530;











