Меры неопределенности суждений
Рассмотрим множество событий, связанных с базой неопределенных знаний, понимаемое как подмножество универсального множества X, называемого достоверным событием. Пустое множество Æ отождествляется с невозможным событием. Предположим, что каждому событию А Ì X можно поставить в соответствие действительное число g(A), задаваемое субъектом. Значение g(A) оценивает степень уверенности, имеющейся у субъекта по отношению к событию A с учетом текущего уровня информированности. По определению величина g(A) растет с увеличением уверенности. Если А - достоверное событие, то g(A) = 1, если А - невозможное событие, то g(A) = 0, т.е.
| g(Æ) = 0 и g(X) = 1. | (1.1) |
Однако g(A)=1 (соответственно 0), вообще говоря, не означает, что А непременно является достоверным (соответственно невозможным) событием.
Наиболее слабой аксиомой для обеспечения минимума согласованности при определении функции множества g является монотонность по включению
| AÍ B ® g(A)£ g(B). | (1.2) |
То есть если событие А влечет за собой событие В, то всегда имеется, по меньшей мере, столько же уверенности в появлении В,сколько в появлении А. Такие функции множества можно использовать для оценки неопределенности, т.е. как меры неопределенности.
Из аксиомы монотонности (1.2), используя объединение AÈ B и пересечение А Ç В событий, можно получить
| " A,BÍ X, g(AÈB)³ max (g(A), g(В)), | (1.3) |
| g(AÇВ) £ min (g(A), g(B)). | (1.4) |
Предельным случаем мер неопределенности оказываются функции множества П такие, что
| " A,B, П(АÈB) = max (П(A), П(B)). | (1.5) |
Они называются мерами возможности (по Л. Заде). Использование термина “возможность” для обозначения этих мер можно обосновать с различных точек зрения.
Первая. Пусть Xi Í X - достоверное событие. Тогда функцию П со значениями {0,1} можно определить удовлетворением условия (1.5) как
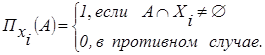
| (1.6) |
Здесь 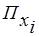 = 1 означает, что событие А возможно.
= 1 означает, что событие А возможно.
Вторая. Если А и 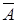 - два противоположных события (
- два противоположных события ( 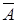 есть дополнение А в X), то имеем
есть дополнение А в X), то имеем
max(П(A), П( 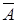 ))=1. ))=1.
| (1.7) |
То есть, из двух противоположных событий, по крайней мере, одно, безусловно, возможно. Более того, когда некоторое событие считается возможным, то не исключена возможность противоположного события. Это согласуется с семантикой суждений о возможности, которые не очень-то обязывают их авторов.
Наконец, условие (1.5) согласуется с представлением о возможности на уровне здравого смысла: для того чтобы рассматривать А È В, достаточно реализовать самый “легкий” вариант из этих двух, например, наименее дорогостоящий.
Когда множество X конечно, то меру возможности П можно определить по ее значениям на одноточечных подмножествах Х:
| П(А) = sup{p(x) / x Î А}, | (1.8) |
где p(x)=П({x}); П естьотображение из X в [0,1], называемое функцией распределения возможностей. Разность между вероятностью и возможностью поясним известным примером:
Пример 1.1. Ганс съедает х яиц за завтраком, где х принимает значения из множества Х {1,2, …, N}. Обозначим возможность (иначе степень легкости) того, что Ганс съедает х яиц как p(х), а вероятность этого события как P(x). Вполне реалистичная картина распределения p(x) и P(x), соответствующая интуитивным представлениям об их смысле, может быть представлена следующим образом:
| Х | ||||||||||
| p(х) | 0,8 | 0,6 | 0,4 | 0,2 | ||||||
| Р(х) | 0,1 | 0,8 | 0,1 |
Обратим внимание на тот факт, что при х=1 и х=3 указанное событие является вполне возможным (p(х)=1), но маловероятным (P(x)=0,1), а при х=4 вполне возможное событие становится невероятным. В то же время невозможность события появляется лишь при х³ 9.
Другой граничный случай мер неопределенности получается при достижении равенства в формуле (1.4). При этом определяется класс функций множества, называемых мерами необходимости N. По аналогии с (1.5)
| " A,B, N(AÇ B) = min (N(A), N(B)). | (1.9) |
Здесь
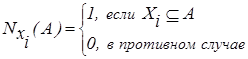
| (1.10) |
и 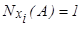 означает, что А - достоверное событие. При этом функция множества N удовлетворяет аксиоме (1.9) тогда и только тогда, когда функция П, определяемая в виде
означает, что А - достоверное событие. При этом функция множества N удовлетворяет аксиоме (1.9) тогда и только тогда, когда функция П, определяемая в виде
" А, П(А) = 1-N( 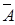 ), ),
| (1.11) |
является мерой возможности. Формула (1.11) есть численное выражение отношения двойственности между модальностями “возможно” и “необходимо”: некоторое событие необходимо, когда противоположное событие невозможно. Это отношение двойственности означает, что всегда можно построить функцию распределения необходимости исходя из функции распределения возможности:
| N(A) = inf{1-p (x) / xÏ A}. | (1.12) |
Меры необходимости удовлетворяют соотношению
min (N(A), N( 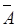 )) = 0, )) = 0,
| (1.13) |
которое исключает одновременную необходимость двух противоположных событий.
На основании (1.7), (1.11) и (1.13) можно получить, что
| " А Í X, П(А) ³ N(A). | (1.14) |
Это условие отражает очевидное утверждение, что, прежде чем быть необходимым, событие должно быть возможным.
Когда имеется информация о появлении события в форме измеренных частот элементарных событий, то мера неопределенности удовлетворяет аксиоме аддитивности:
| " А,В, АÇВ = 0, P(AÈB) = P(A)+P(B), | (1.15) |
т.е. становится вероятностной мерой. Формула (1.15) - вероятностный эквивалент аксиом (1.5) и (1.9), а условие, эквивалентное условиям (1.8) и (1.12),
Р(А) = 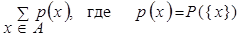 . .
| (1.16) |
Аналогом соотношений (1.7) и (1.13) является известное из теории вероятностей соотношение
P(A) + P( 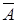 ) = 1, ) = 1,
| (1.17) |
в то время как из (1.7) и (1.13) следуют лишь неравенства
N(A) + N( 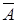 ) £ 1, ) £ 1,
| (1.18) |
П(А) + П( 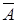 ) ³ 1. ) ³ 1.
| (1.19) |
Из этих соотношений видно одно из главных отличий возможности от вероятности: вероятность некоторого события полностью определяет вероятность противоположного события, а возможность (или необходимость) некоторого события и возможность (необходимость) противоположного события связаны слабее. В частности, для того, чтобы охарактеризовать неопределенность по отношению к событию А, требуется два числа N(A) и П(А). Это очень важно, когда моделируются не реальные физические явления, а субъективные суждения (даже о тех же явлениях). При этом представляется вполне естественным стремление не устанавливать жесткие связи между показателями, свидетельствующими в пользу некоторого события (степень необходимости), и показателями, свидетельствующими против него (степень возможности).
Меры возможности и необходимости можно построить даже при сохранении требования аддитивности. Пусть X1, X2,..., Xn непустые, попарно различные подмножества конечного множества X, с соответствующими значениями вероятности p(X1), p(X2),..., p(Xn), такими, что
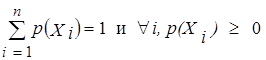 . .
|
Величина p(Xi) понимается как значение вероятности совокупности элементарных событий, составляющих Xi. Подмножества Xi называют фокальными элементами, отражающими неточность наблюдений. Тогда вероятность события А можно охарактеризовать лишь неточно как величину, содержащуюся в интервале [P (A), 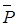 (A)] с границами
(A)] с границами
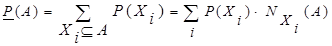
| (1.20) |
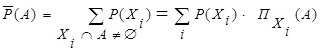 . .
| (1.21) |

Значение P (A) вычисляется по всем фокальным элементам, которые делают необходимым появление события А. Значение 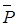 (A) получается при рассмотрении всех фокальных элементов, которые делают возможным появление события А.
(A) получается при рассмотрении всех фокальных элементов, которые делают возможным появление события А.
Между 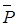 и P имеется отношение двойственности
и P имеется отношение двойственности
" A, 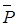 (A)= 1 - P (А). (A)= 1 - P (А).
| (1.22) |
Доказано, что функция 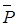 (A) удовлетворяет аксиоме (1.5), т.е. является мерой возможности, а функция P (A) - аксиоме (1.9) и является мерой необходимости, если фокальные элементы образуют последовательность вложенных множеств X1ÌX2Ì.... ÌXn... Так функция распределения возможностей определяется:
(A) удовлетворяет аксиоме (1.5), т.е. является мерой возможности, а функция P (A) - аксиоме (1.9) и является мерой необходимости, если фокальные элементы образуют последовательность вложенных множеств X1ÌX2Ì.... ÌXn... Так функция распределения возможностей определяется:
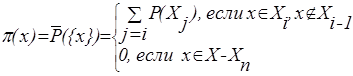 . .
|
Если фокальные элементы являются элементарными событиями, то P(A) = 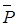 (A) = P(A), т.е. приходим к вероятностной мере.
(A) = P(A), т.е. приходим к вероятностной мере.
Формулы (1.20) и (1.21) позволяют считать, что функция распределения возможностей распределяет класс вероятностных мер P, такой, что
| P= {P½"A, N(A )£ P(A) £ П(А)}. | (1.23) |
Если схематично представить базу знаний с помощью множества фокальных элементов (которые являются составляющими “значения” в наборе, описывающем информационную единицу: объект, признак, значение, уверенность), то легко понять, что вероятностные меры соответственным образом синтезируют базу точных дифференцированных (до элементарного события) знаний (данных), тогда как меры возможности суть отражения неточных, но связанных, т.е. подтверждающих друг друга знаний. Функции возможности в этом смысле более естественны для представления чувства неуверенности: от субъекта не ждут слишком точной информации, но желают услышать по возможности наиболее связанные суждения. Зато точные, но флуктуирующие данные чаще всего получают из наблюдений и измерений физического явления. В связи с этим отражение реального мира через физический эксперимент наиболее целесообразно осуществлять средствами теории вероятностей и математической статистики, базирующимися на теории четких множеств, а в отражении реального мира через суждения субъектов (экспертов) разумнее использовать теорию возможностей, органично сочетающуюся с теорией нечетких множеств.
Контрольные вопросы
| 1. | Как преодолеть путь от “неизвестности” к “определенности?” |
| 2. | В чем заключается принципиальное отличие физической (объектной) неопределенности от лингвистической (субъектной) неопределенности? |
| 3. | Что такое “нечеткость”? Какова ее природа? |
| 4. | Что оценивает мера неопределенности? |
| 5. | Что подразумевается под мерой возможности? |
| 6. | В каком соотношении находятся модальности “возможность” и “необходи-мость”, их меры? |
| 7. | Определите различие между “возможностью” и “вероятностью”. |
| 8. | Сопоставьте меры возможности, вероятности и необходимости. |
Дата добавления: 2021-10-28; просмотров: 454;











