Электромагнитная индукция

1. Электромагнитная индукция – это явление, состоящее в том, что изменяющееся магнитное поле создаёт в замкнутых проводниках электрические токи. ЭДС, возбуждающую эти токи, называют электродвижущей силой индукции, а токи – индукционными. Явление электромагнитной индукции открыл Майкл Фарадей в 1831 г.

В основе открытия Фарадея лежат результаты многочисленных опытов, выполненных им в течение 9 лет. Укажем 4 наиболее характерные группы.

Опыт 1. На деревянную катушку были намотаны изолированным медным проводом две обмотки длинной по 203 фута (» 61 м) каждая. Концы одной обмотки присоединялись к тангенс-гальванометру, концы другой – к химическому источнику тока (к батарее из элементов Вольты) через ключ (рис.109). При замыкании ключа стрелка гальванометра отклонялась на короткое время в одну сторону, при размыкании – в другую.

Опыт 2. Повторяет 1-й с той разницей, что обмотки наматывались на замкнутый железный сердечник (рис.110). По сравнению с деревянной катушкой эффект значительно усиливался. Этот опыт считается решающим.

Опыт 3. Повторяет опыт 1-й с той разницей, что обмотки наматывались на картонную трубку (рис.111). Если трубка пустая, эффект такой же, как в первом опыте. Если в трубку опускался железный стержень, эффект усиливался. Если опускался медный стержень, эффект по сравнению с первым опытом практически не изменялся.

Опыт 4. Повторяет опыт 3-й с той разницей, что ключ обмотки с элементом Вольты не замыкался, а внутри картонной трубки двигался вверх-вниз постоянный магнит. При движении магнита вниз стрелка гальванометра отклонялась в одну сторону, при движении магнита вверх - в другую. При изменении полюсов магнита направления отклонения стрелки менялись (рис.112).

По результатам своих опытов Фарадей сделал вывод: в замкнутом проводнике индукционный ток возникает в том случае, когда проводник или какая-либо его часть пересекает линии магнитной индукции.

2. Закон электромагнитной индукции. Формулировка Фарадея, 1831 г. : заряд, переносимый индукционным током через поперечное сечение проводника, пропорционален количеству силовых линий Ф, пересекаемых проводником q = k Ф. (16.1)

Здесь Ф – число силовых линий, в современной терминологии – магнитный поток, k – коэффициент пропорциональности.

В 1834 г. Эмилий Ленц дополнил формулировку Фарадея правилом:

индукционный ток во всех случаях направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток.

В 1873 г. Джеймс Максвелл в фундаментальном “Трактате об электричестве и магнетизме” дал современную формулировку закона электромагнитной (магнитоэлектричес-кой по Максвеллу) индукции. В СИ формула закона имеет вид: 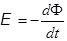. (16.2)

ЭДС индукции E, возникающая в контуре, пропорциональна скорости изменения магнитного потока, пронизывающего площадь этого контура. Формулировка Максвелла включает в себя и закон индукции в формулировке Фарадея, и правило Ленца.

а. Формулировки Фарадея получается при вычислении заряда q, протекающего через поперечное сечение замкнутого проводника. Индукционный ток в проводнике i = E çR = - (dФ ç dt) ç R , где R – сопротивление проводника. Допустим, в начальный момент времени площадку контура пронизывал поток Ф, в конечный момент – поток 0. Для этого достаточно контур повернуть на 90° (рис.113). Так как dq = idt , то

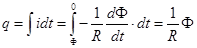. (16.3)

Коэффициент k в формуле (16.1) представляет собой электрическую проводимость контура, k = 1çR.

б. Правило Ленца. Рассмотрим круговой замкнутый контур. Вектор нормали n к его площадке согласуем с направлением обхода правилом правого винта (рис.114). Этот вектор n задаёт направление силовых линий B через площадку.

Допустим, магнитный поток Ф через площадку увеличивается. Это значит, что линии B приходят из бесконечности и сгущаются внутри площадки. Производная dФçdt > 0 (поток увеличивается). ЭДС индукции E = - (dФçdt). Знак минус здесь означает, что ЭДС индукции противоположна направлению обхода. Индукционный ток так же противоположен направлению обхода, а силовые линии его магнитного поля противоположны линиям внешнего поля B. Потому поле индукционного тока ослабляет внешнее поле B, препятствуя его нарастанию. Таким образом, знак “минус” в формуле (16.2) выражает правило Ленца.

Если магнитный поток Ф через площадку контура убывает, силовые линии разбегаются от центра к бесконечности, то dФçdt < 0, а E = - dФçdt > 0. Индукционный ток совпадает с направлением обхода, его магнитное поле усиливает внешнее поле B, препятствуя его убыванию.

Как показали многочисленные опыты, величина ЭДС индукции не зависит от материала проводника. Она определяется исключительно скоростью изменения пронизывающего его магнитного потока.

3. Электромагнитная индукция и сохранение энергии. Проанализируем баланс энергии в явлении электромагнитной индукции. Для этого рассмотрим движение проводника с током в магнитном поле.

Допустим, проводник длинной l может скользить в однородном магнитном поле по проводникам, присоединённым к полюсам источника постоянного тока с ЭДС E ₀ (рис.115). Подвижный проводник замыкает цепь, её сопротивление постоянно и равно R , ток в цепи i.

Для простоты полагаем, что сам проводник и направление его движения перпендикулярны вектору B. Работа перемещения проводника под действием силы Ампера F есть 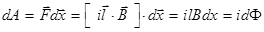. (16.4)

Здесь dФ = Bldx = BdS – магнитный поток, пересечённый проводником при его перемещении на расстояние dx.

Поскольку сила Ампера складывается из сил Лоренца, не изменяющих энергию движения зарядов, то работа перемещения проводника может совершаться не за счёт энергии магнитного поля, а за счёт энергии источника тока с ЭДС E ₀. Приняв во внимание тепло Джоуля – Ленца, выделяющееся в проводнике, полная работа источника тока равна

E ₀idt = i²Rdt + idФ. (16.5)

Разделив обе части равенства на iRdt и разрешив его относительно тока i, получаем:

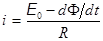. (16.6)

Очевидно, - dФçdt – ЭДС индукции. Она направлена на встречу ЭДС источника тока и уменьшает ток в цепи.

Формулу (16.6) получил Герман Гельмгольц в 1847 г. Она позволяет рассматривать закон электромагнитной индукции как следствие закона сохранения энергии.

Чем быстрее скользит проводник, тем больше линий B он пересекает, тем больше ЭДС индукции, тем меньше ток в цепи. И наоборот. Эта ситуация реализуется в якорях электрических двигателей. Чем больше нагрузка, тем медленнее вращается якорь, тем меньше возникающая в нём ЭДС индукции. Поэтому ток, протекающий по якорю, велик. Велика и потребляемая двигателем мощность.

С уменьшением нагрузки скорость вращения якоря увеличивается, увеличивается так же и ЭДС индукции, уменьшающая ток в цепи, и потребляемая двигателем мощность падает.

Механизм работы источника тока по перемещению проводника в магнитном поле состоит в следующем. Допустим, в проводнике есть свободные положительные и отрицательны заряды. Электрическое поле источника тока E направлено вдоль по проводнику (ось ОХ, рис.116). Оно разгоняет свободные заряды до некоторой скорости v, совершая работу mv²ç2.

Если проводник находится в магнитном поле B (на рис.116 линии B направлены “от нас”), на заряды действует сила Лоренца f_m. Траектория движения зарядов искривляются в одну сторону. В результате наряду с составляющей импульса mv_x появляется нормальная к оси проводника составляющая mv_y. При соударении зарядов с узлами решётки именно эта составляющая создаёт силу Ампера.

Если проводник движется под действием этой силы, свободные заряды под действием этой силы, свободные заряды сталкиваются с “убегающими” узлами. Поэтому даже при упругом ударе их энергия после соударения уменьшается. Часть её идёт на совершение работы по перемещению проводника.

4. Вихревые токи Фуко. Если массивный проводник находится в быстро переменном магнитном поле, то благодаря его малому электрическому сопротивлению под действием ЭДС индукции в нём могут возбуждаться большие индукционные токи. Эти токи обнаружил по нагреванию проводников в 1855 г. Жан Фуко.

Токи Фуко тормозят движение проводников в магнитном поле. Они возникают в любом случае, когда изменяется магнитный поток, пронизывающий проводник.

В индукционных электропечах тепло индукционных токов используется для плавки металлов. В бытовых микроволновых печах – для приготовления пищи.

Выделение же тепла в магнитопроводах нежелательно. С целью его уменьшения сердечники трансформаторов, якоря и статоры электродвигателей набирают из отдельных покрытых оксидным слоем тонких стальных пластин, а на высоких частотах используют сердечники из ферритов с большим удельным сопротивлением.

5. Самоиндукция. Каждый контур, по которому идёт ток, создаёт магнитное поле, а поэтому пронизывается магнитным потоком собственного поля. Величина этого потока Ф пропорциональна току i, протекающему по контуру. Ф = L·i. (16.7)

Коэффициент пропорциональности L называют коэффициентом самоиндукции или индуктивностью контура.

При изменении тока в контуре изменяется и пронизывающий его магнитный поток. В результате в контуре наводится ЭДС самоиндукции. 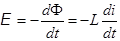. (16.8)

Знак минус здесь показывает, что направление ЭДС самоиндукции противоположно направлению изменения тока. В результате изменение тока в контуре замедляется.

Например, если ток в контуре убывает, то возникающая ЭДС самоиндукции при этом направлена по току. Она препятствует уменьшению тока.

Если же ток в контуре возрастает, то ЭДС самоиндукции направлена против тока. Она тормозит нарастание тока.

Наличие индуктивности приводит к тому, что контур приобретает электрическую инертность. Она состоит в том, что любое изменение тока в контуре тормозится тем сильнее, чем больше индуктивность контура L.

Этот факт хорошо иллюстрируется опытом А. Эйхенвальда. Две одинаковые лампочки Л₁ и Л₂ (6,3 В, 0,28 А) подключены параллельно к источнику постоянного тока с ЭДС E ₀ = 6 В. Последовательно с одной из ламп (Л₂ на рис.117) включена катушка на 3000-4000 витков. При замыкании цепи ключом Кл хорошо видно, что лампа Л₂ загорается позже лампы Л₁.

Явление самоиндукции открыл в 1832 г. Джозеф Генри. Его именем названа единица индуктивности в СИ. Определение её можно дать на основе формулы (16.8):

один генри (1 Гн) – это индуктивность такого контура, при изменении тока в котором со скоростью 1 А в секунду в контуре наводится ЭДС индукции 1 В.

6. Индуктивность тороидального соленоида. Пусть на тороидальный сердечник с магнитной проницаемостью μ и длиной осевой линии l намотано N витков изолированного провода (рис.118). Если по виткам катушки идёт ток I, то, как показано в примере 13.2 на с.__, магнитная индукция поля в сердечнике равна 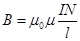. (16.9)

Магнитный поток, пронизывающий каждый виток, равен BS, а поток, через все витки, в N раз больше, 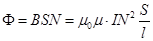. (16.10)

Здесь S – площадь сечения сердечника.

Этот же магнитный поток можно определить ещё как магнитный поток произвольного контура с индуктивностью L, то есть Ф = LI. Отсюда 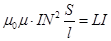; Þ 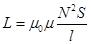. (16.11)

Индуктивность катушки растёт пропорционально квадрату числа витков N² и проницаемости сердечника m.

Эта формула применима так же для вычисления индуктивности L отрезка длинной l бесконечно длинного соленоида сечением S, содержащего на этом отрезке N витков.

7. Энергия магнитного поля. Если ток в контуре изменяется на величину di, то магнитный поток поля этого тока изменяется на величину dФ = Ldi. Но это изменение потока dФ сопряжено с работой тока dA = idФ.

Если ток увеличивается, то работа тока идёт на увеличение энергии контура с током, так что dA = dW. Отсюда dW = dA = idФ = Lidi. При увеличении тока от 0 до I энергия контура найдётся интегрированием: 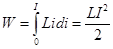. (16.12)

Итак, контур индуктивностью L, по которому протекает ток I, имеет запас энергии LI²ç2. Это энергия магнитного поля, придающая электрическую инертность контуру. При замыкании цепи требуется время на накапливание этой энергии, а при размыкании – время на её расходование. Мерой электрической инертности контура является его индуктивность.

8. Плотность энергии магнитного поля. Для её вычисления рассмотрим секцию бесконечно длинного соленоида длинной l. Полагаем, что на этом отрезке l намотано N витков, магнитная проницаемость сердечника соленоида m, его сечение S (рис.119).

Поскольку соленоид бесконечно длинный, то всё магнитное поле, создаваемое этим соленоидом, находится внутри его. Магнитное поле, создаваемое током I, идущим по N виткам на отрезке длинной l, полностью заключено внутри объёма V = l S этого отрезка.

Энергия магнитного поля, заключённого в этом объёме V = l S, равна

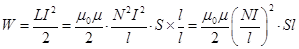. (16.13)

Разделив на объём Sl, получаем плотность энергии магнитного поля в соленоиде 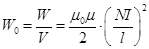. (16.14)

Комбинацию параметров в скобках NIçl можно выразить из формулы (13.10), определяющей индукцию магнитного поля в бесконечно длинном соленоиде. Подставив в (16.14), получаем: 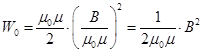. (16.15)

Если в пространстве существуют одновременно электрическое и магнитное поля, то объёмная плотность энергии электромагнитного поля в целом равна сумме энергий электрического (7.22) и магнитного (16.15) поля: 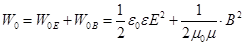. (16.16)