Расчет общей передаточной функции системы
Поставим задачу нахождения передаточной функции любого j-го сигнала схемы по любому i-му сигналу 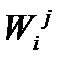 .Очевидно, что
.Очевидно, что
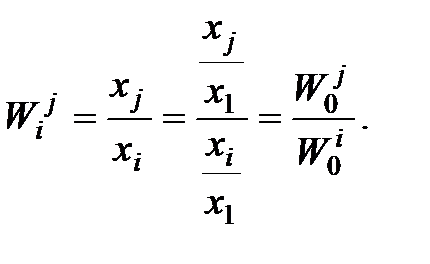 (2.8)
(2.8)
Таким образом, задачу нахождения 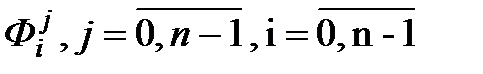 , можно свести к нахождению
, можно свести к нахождению 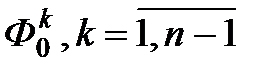 .
.
Рассмотрим метод нахождения основной передаточной функции системы 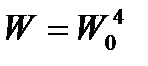 .
.
Суть данного метода заключается в следующем:
1) Рассчитывается определитель 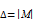 . Этот определитель будет являться знаменателем главной передаточной функции [1]. При его расчете используется метод приведения матрицы
. Этот определитель будет являться знаменателем главной передаточной функции [1]. При его расчете используется метод приведения матрицы 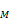 треугольному виду (метод Гаусса) [1]. Данный метод заключается в том, что с помощью линейных операций над строками матрицы искусственно обнуляются элементы либо под, либо над главной диагональю (в данном случае последнее является более предпочтительным). Обнуление начинается от крайнего правого столбца до тех пор, пока не будет получен определитель такого порядка, который можно легко рассчитать (например, 3х3).
треугольному виду (метод Гаусса) [1]. Данный метод заключается в том, что с помощью линейных операций над строками матрицы искусственно обнуляются элементы либо под, либо над главной диагональю (в данном случае последнее является более предпочтительным). Обнуление начинается от крайнего правого столбца до тех пор, пока не будет получен определитель такого порядка, который можно легко рассчитать (например, 3х3).
Определитель исходной матрицы M сводится к виду
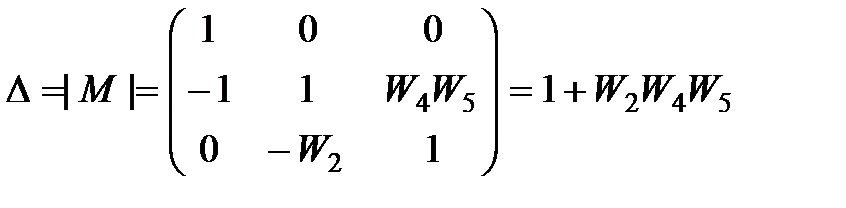 . (2.8)
. (2.8)
2) Для того, чтобы рассчитать числитель передаточной функции, формируется матрица столбец  : столбец, соответствующий номеру выхода, обнуляется, а единственная единица заносится в строку, соответствующую номеру входа [1]. Далее расчет определителя осуществляется аналогичным образом.
: столбец, соответствующий номеру выхода, обнуляется, а единственная единица заносится в строку, соответствующую номеру входа [1]. Далее расчет определителя осуществляется аналогичным образом.
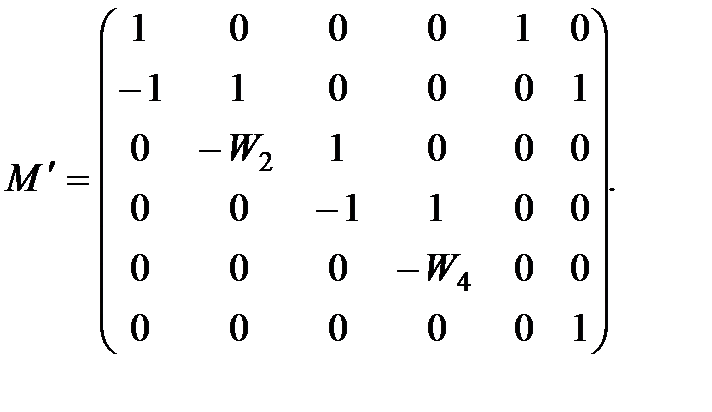 (2.9)
(2.9)
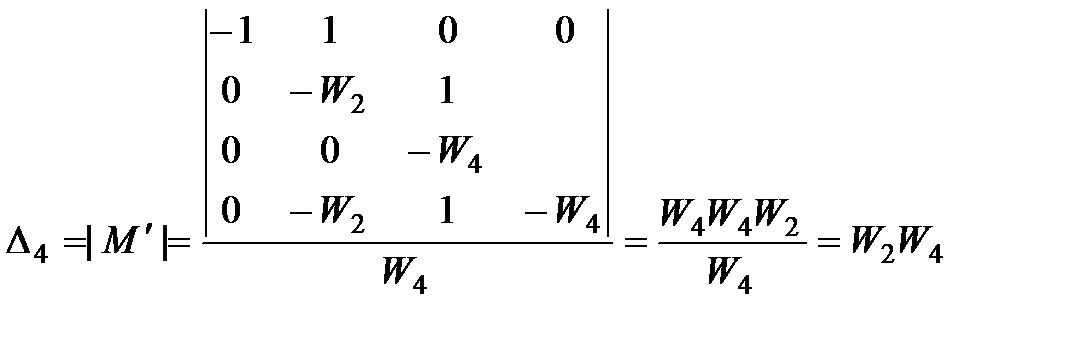 (2.10)
(2.10)
3) Рассчитывается передаточная функция системы:
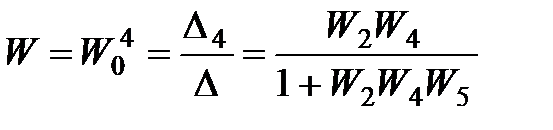 . (2.11)
. (2.11)
Как видно из (2.11) полученный результат идентичен передаточной функции, которая может быть получена методом структурных преобразований исходной схемы.
Метод составления определителя позволяет найти передаточную функцию любого сигнала по любому, является легко формализуемым и реализуемым на компьютере. В связи с этим в литературе можно встретить название «машинный метод расчета» [5,7].
Основной сложность при реализации данного метода является необходимость вычисления не обычного определителя, содержащего числа, а определителя, содержащего элементы «0», «1», «–1», «–Wi» и преобразуемые из них величины.
Для преодоления описанных ограничений и решения поставленной задачи были разработаны структуры данных и алгоритмы, поддерживающие не численную, а символьную арифметику.
Ограничение линейности на функциональные зависимости между передаточными функциями звеньев определило реализацию следующих структур данных:
1) «Произведение»: 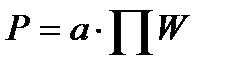 , где
, где 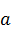 – целое число – коэффициент произведения,
– целое число – коэффициент произведения, 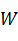 – одна из передаточных функций системы (примеры: «-1», «1», «0», «
– одна из передаточных функций системы (примеры: «-1», «1», «0», « 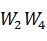 »);
»);
2) Сумма произведений: 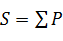 , где P – «Произведение» (пример: «
, где P – «Произведение» (пример: « 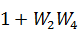 »);
»);
3) Произведение сумм: 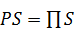 , где S – «Сумма произведений».
, где S – «Сумма произведений».
Для произведения символьных линейных операций над данными структурами данных были реализованы следующие функции:
1) умножение на целое число;
2) умножение;
3) суммирование;
4) приведение подобных членов;
5) деление (сокращение дробей).
Набор данных функций позволяет не только находить передаточную функцию системы, но и по возможности минимизировать ее, достигая результата, который может быть получен человеком при использовании метода структурных преобразований.
Дата добавления: 2021-10-28; просмотров: 459;











