Нахождение корней характеристического уравнения методом Берстоу
В разделах 2.3.1-2.3.2 был осуществлен вывод передаточной функции САР по ее структурной схеме, как зависимости от передаточной функции звеньев системы 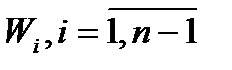 , где n – число сигналов системы.
, где n – число сигналов системы.
Так как главная передаточная функция САР
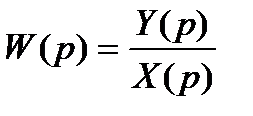 , (2.14)
, (2.14)
где X(p) и Y(p) – изображения по Лапласу соответственно входной и выходной величин
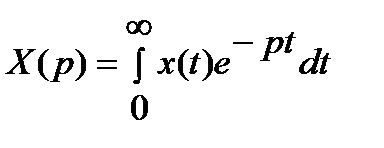 ;
; 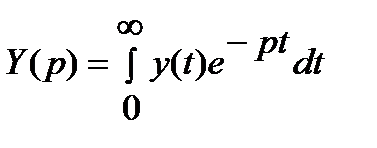 ,
,
то для входного единичного ступенчатого воздействия 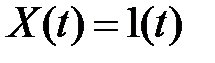 :
:
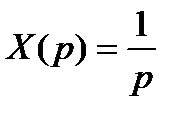 ,
,
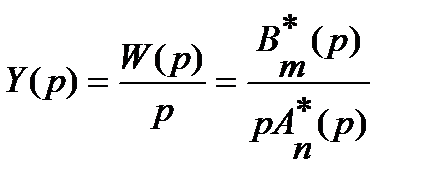 . (2.15)
. (2.15)
Окончательно для изображения выходной величины получим:
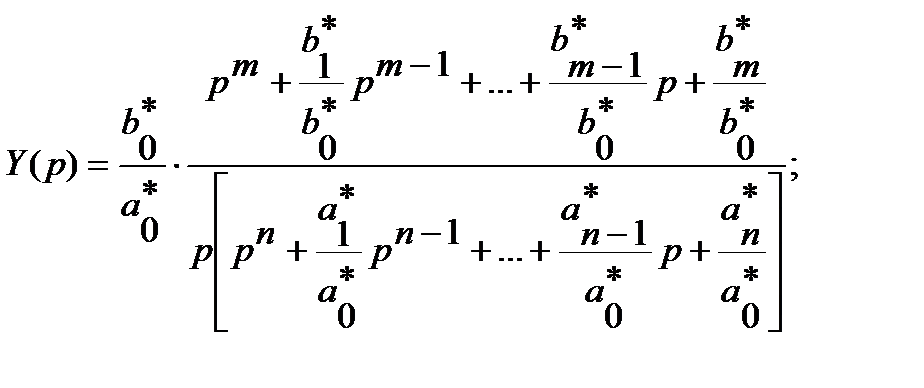
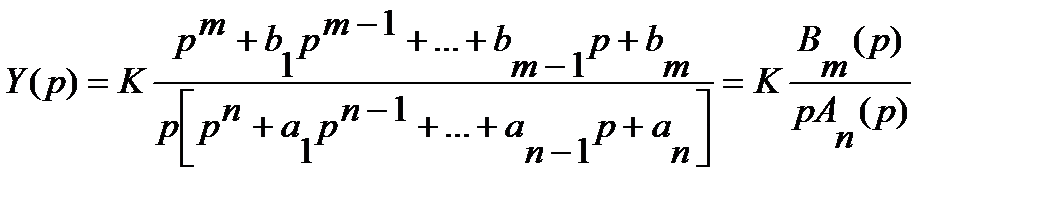 , (2.16)
, (2.16)
где
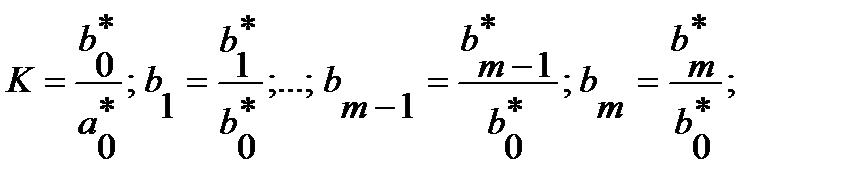
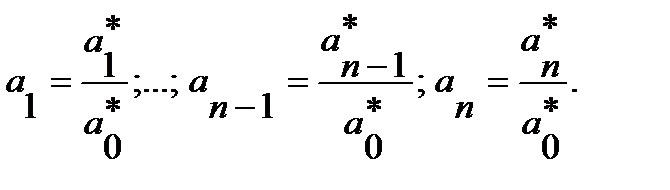
Для аналитического получения переходного процесса в системе сначала нужно найти корни знаменателя (характеристического уравнения САР) 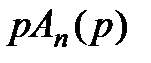 . Один корень
. Один корень 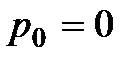 , а остальные n корней являются корнями полинома
, а остальные n корней являются корнями полинома 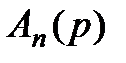 . Одним из методов нахождения любых (действительных или комплексно-сопряженных) корней полинома произвольной степени является численный метод Берстоу [1].
. Одним из методов нахождения любых (действительных или комплексно-сопряженных) корней полинома произвольной степени является численный метод Берстоу [1].
Сущность метода заключается в следующем. Из исходного полинома 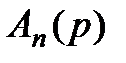 выделяется приведенный квадратный трехчлен. Если корни квадратного трехчлена
выделяется приведенный квадратный трехчлен. Если корни квадратного трехчлена 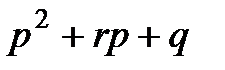 являются корнями исходного полинома,
являются корнями исходного полинома, 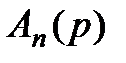 то
то 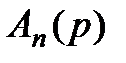 должно делиться на
должно делиться на 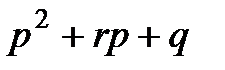 без остатка [1].
без остатка [1].
Таким образом, исходный полином представляется как
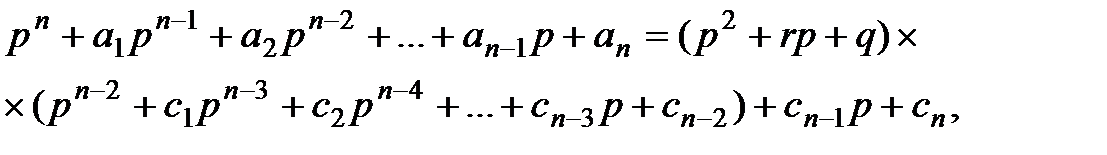 (2.17)
(2.17)
где
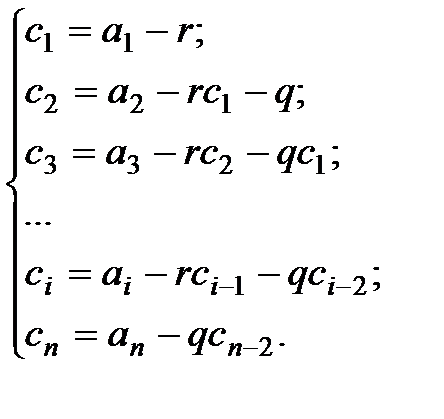 (2.18)
(2.18)
Деление без остатка означает, что коэффициенты 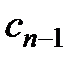 и
и 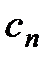 должны быть равны нулю. Как видно из формулы (2.18) коэффициенты
должны быть равны нулю. Как видно из формулы (2.18) коэффициенты 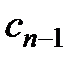 и
и 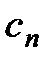 являются функциями коэффициентов трехчлена r, q и коэффициентов исходного полинома
являются функциями коэффициентов трехчлена r, q и коэффициентов исходного полинома 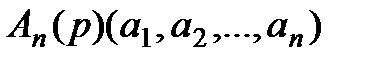 :
:
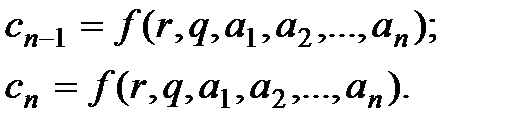
Так как коэффициенты исходного полинома 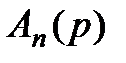 в общем случае неизвестны, то необходимо исследовать зависимость
в общем случае неизвестны, то необходимо исследовать зависимость 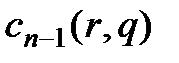 ,
, 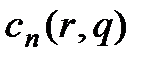 .
.
Для нахождения корней методом Берстоу необходимо выбрать начальное приближение для коэффициентов трехчлена r и q. Затем значения коэффициентов r и q уточняются с помощью коррекции
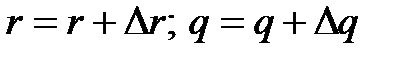 (2.19)
(2.19)
Требуется, чтобы остаточные члены, 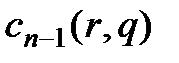 ,
, 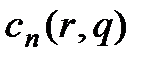 обращались в ноль в процессе вычисления. Если эти функции разложить в ряд Тейлора в окрестности точки
обращались в ноль в процессе вычисления. Если эти функции разложить в ряд Тейлора в окрестности точки 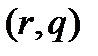 , то получим:
, то получим:
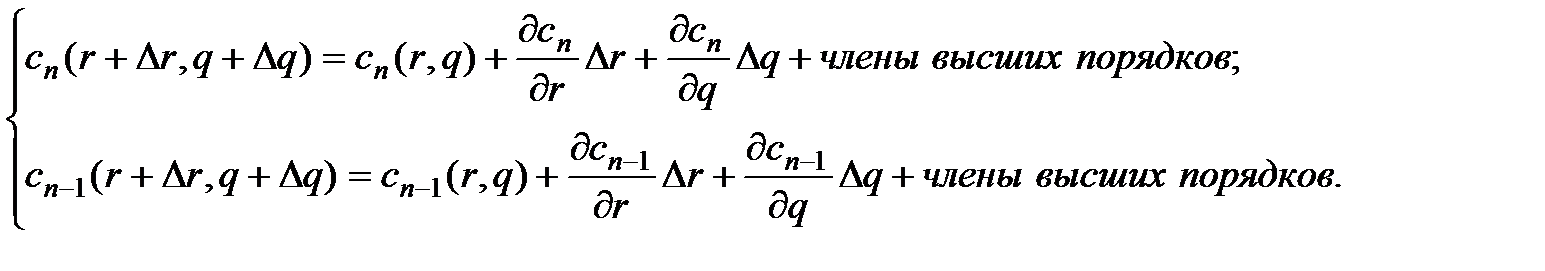 (2.20)
(2.20)
Если предположить, что при уточнении r и q остаточные члены близки к нулю, то левые части этих уравнений обратятся в нуль. Тогда, решая (2.20) относительно 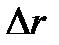 и
и 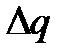 и пренебрегая членами более высоких порядков, получим:
и пренебрегая членами более высоких порядков, получим:
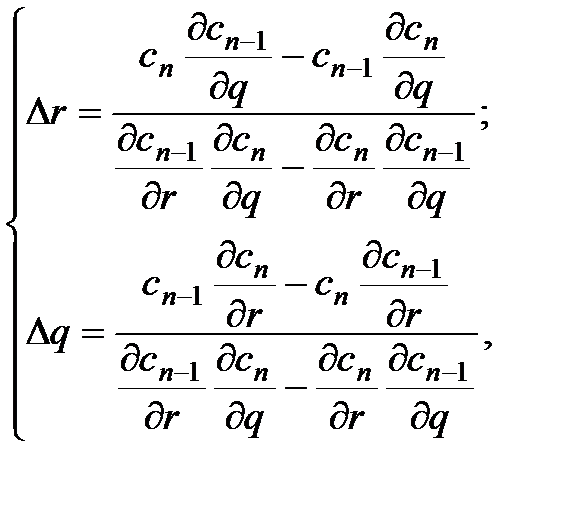 (2.21)
(2.21)
где 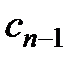 и
и 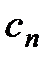 являются функциями
являются функциями 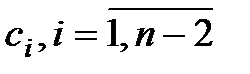 , которые в свою очередь зависят от r и q.Поэтому необходимо получить последовательность частных производных
, которые в свою очередь зависят от r и q.Поэтому необходимо получить последовательность частных производных 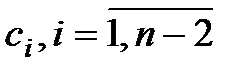 продифференцировав коэффициенты в формуле (2.18) по r и q. Получим:
продифференцировав коэффициенты в формуле (2.18) по r и q. Получим:
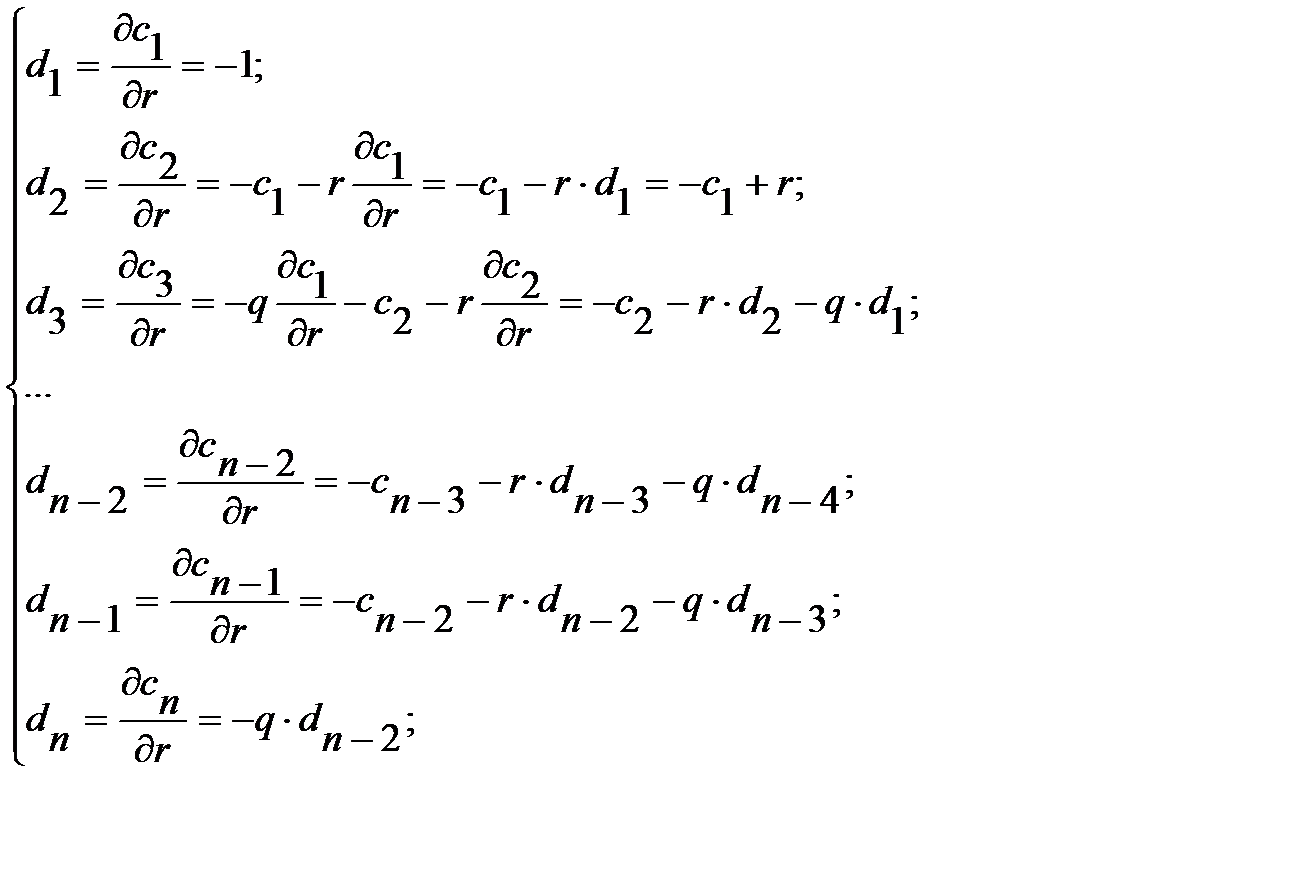 (2.22)
(2.22)
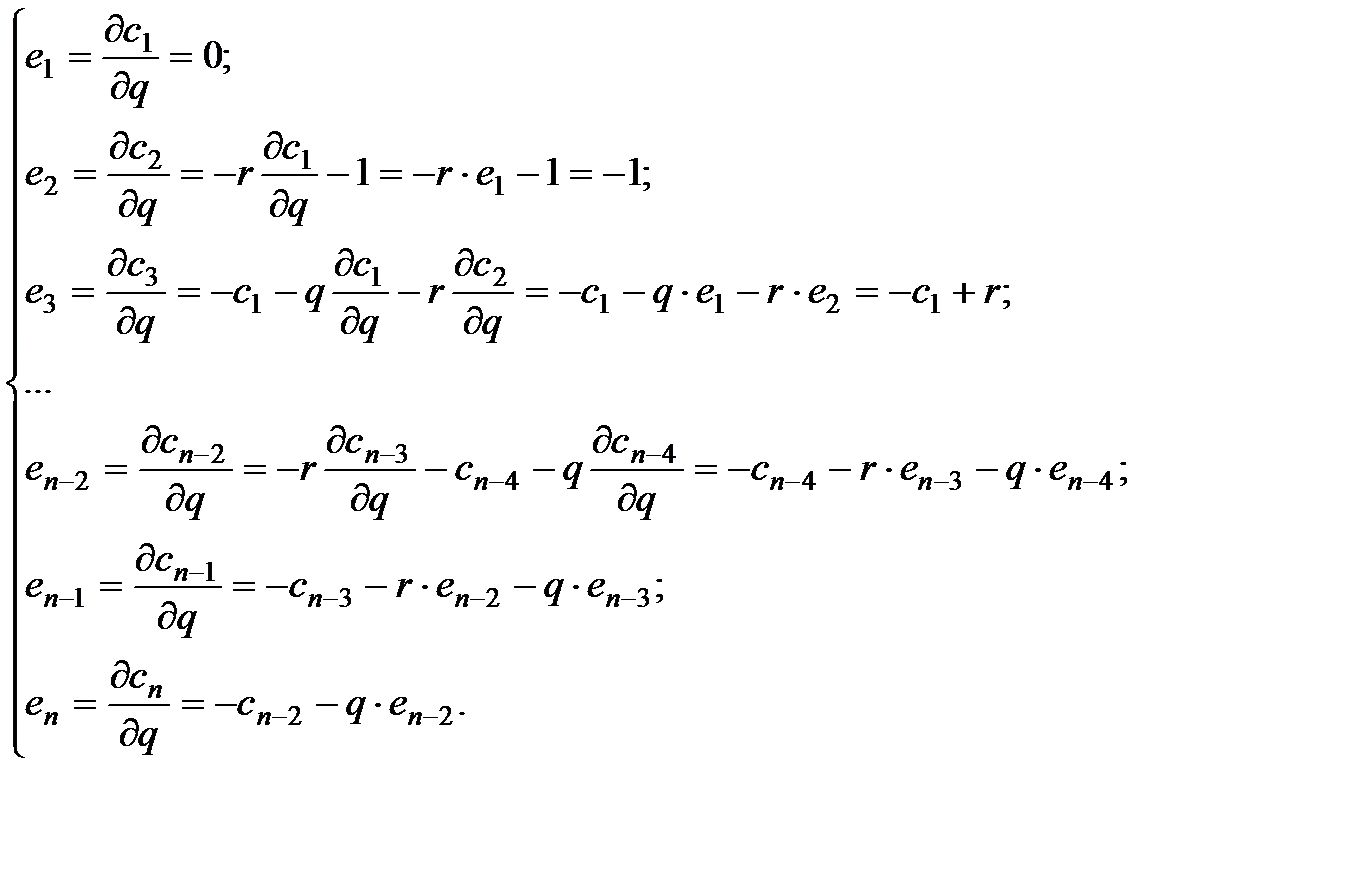 (2.23)
(2.23)
Производные 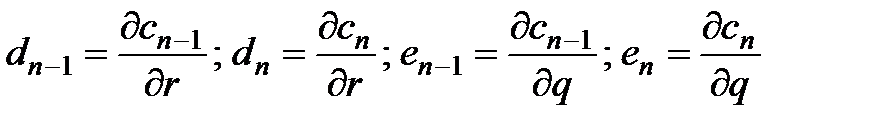 используются для коррекции коэффициентов по формулам (2.21).Вычисления коэффициентов r и q по выражениям (2.21), (2.19) ведутся до тех пор, пока полученные значения коэффициентов
используются для коррекции коэффициентов по формулам (2.21).Вычисления коэффициентов r и q по выражениям (2.21), (2.19) ведутся до тех пор, пока полученные значения коэффициентов 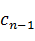 и
и 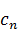 не будут равны нулю с некоторой точностью
не будут равны нулю с некоторой точностью 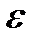 :
:
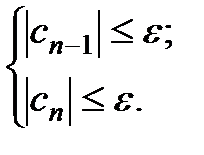 (2.23)
(2.23)
Это означает, что корни трехчлена 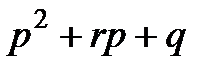 являются с некоторой точностью
являются с некоторой точностью 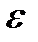 корнями исходного полинома
корнями исходного полинома 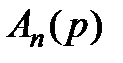 .
.
После нахождения пары корней
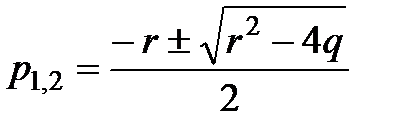 , (2.24)
, (2.24)
трехчлен исключается из 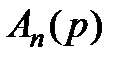 , и процедура повторяется для полинома степени
, и процедура повторяется для полинома степени 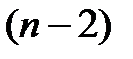 , являющегося результатом деления в формуле (2.18):
, являющегося результатом деления в формуле (2.18):
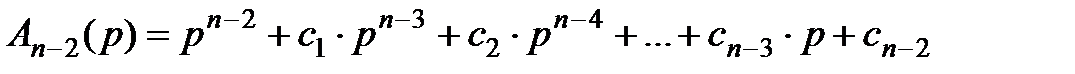 . (2.25)
. (2.25)
Если порядок полинома 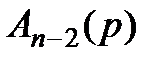 меньше или равен двум, то вычисление корней заканчивается, а оставшиеся корень или два корня находят из решения линейного или квадратного уравнения. В результате получим все корни полинома
меньше или равен двум, то вычисление корней заканчивается, а оставшиеся корень или два корня находят из решения линейного или квадратного уравнения. В результате получим все корни полинома 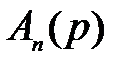
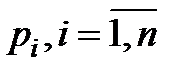 .
.
Дата добавления: 2021-10-28; просмотров: 521;











