Моделирование непрерывных динамических систем

Как уже отмечалось в разделе 2.1, стандартным представлением непрерывной динамической системы в системах моделирования является структурная схема, которой соответствует система дифференциальных уравнений или система алгебро-дифференциальных уравнений.

Моделирование непрерывной системы подразумевает итеративный расчет всех координат системы при изменении модельного времени. Таким образом, механизм моделирования сводится к вызову процедур расчета отдельных динамических звеньев системы, которые позволяют по известным входным сигналам блока, рассчитать его выходные сигналы. Определение порядка вызова функций блоков определяется математическим ядром и будет подробнее рассмотрено в разделе 3.7.

Рассмотрим методы моделирования наиболее важных динамических звеньев непрерывных систем.

Численные методы решения дифференциальных уравнений

Основные динамические звенья непрерывных динамических систем реализуют определенное дифференциальное уравнение. Рассмотрим наиболее простые методы численного решения дифференциальных уравнений (методы интегрирования).

Будем считать, что исходное ДУ звена представлено в форме Коши:

.

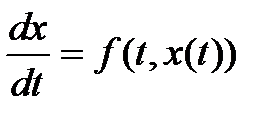Начальное значение функции .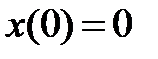

Метод Эйлера

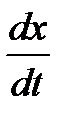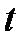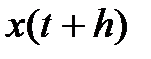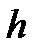Метод Эйлера является простейшим методом интегрирования. Его суть заключается в том, что по известной производной в момент времени рассчитывается значение функции , где – шаг интегрирования:

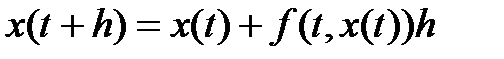. (2.30)

Геометрической интерпретацией метода Эйлера является построение ломаной прямой искомой функции (рис. 2.4).

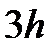
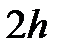
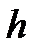
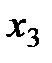
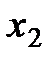
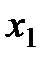
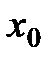
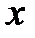
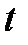
Рис. 2.4 Геометрическая интерпретация метода Эйлера

Метод Эйлера – единственный метод, который позволяет заранее (за шаг) рассчитать значение искомой функции, но он обладает самой большой ошибкой

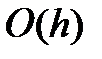- первый порядок ошибки.