Математическое описание простой непрерывной динамической системы

Примером непрерывной динамической системы является система автоматического регулирования (САР). Она может быть представлена системой алгебро-дифференциальных уравнений (ДУ).

Если поставлена задача составления исходных ДУ САР, то возможны две ситуации: либо детальная декомпозиция системы на модули и отдельные звенья возможна, либо нет.

Если декомпозиция возможна, то, опираясь на постулаты о сохранении материи и энергии (для соответствующего энергетического домена) и на закон Ома (в соответствующей формулировке), приступают к составлению исходных ДУ САР, т.е. к созданию истинной модели системы. Истинной будем называть такую модель или такое математическое описание, о которых известно, что они детально соответствуют физической природе системы.

Если декомпозиция на модули и звенья для системы невозможна, то, не имея детальной информации о ее физической природе, можно получить лишь ложную модель или ложное математическое описание, которые, однако, позволят исследовать систему и получить адекватные результаты. В этом случае совокупность исходных ДУ САР получают через частотный домен, путем экспериментального снятия частотных характеристик.

Для физической системы порядок системы ДУ ее истинной модели обычно в десять и более раз выше порядка системы ДУ ее ложной модели (например, для моделей ОУ). Тем обусловлена широкая популярность ложных моделей, и типовых звеньев, как структурных элементов для их создания.

Общая форма записи систем ДУ:

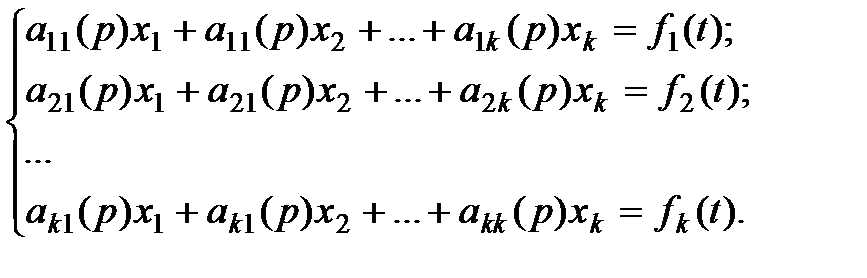(2.1)

где:

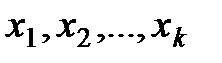- обобщенные координаты системы, в том числе (для САР) ошибка - x(t) и регулируемая величина - y(t);

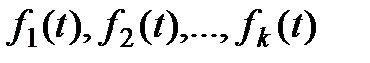- внешние координаты - задающие g(t) и возмущающие f(t) воздействия.

Для удобства и формализации решений систему уравнений (2.1) можно представить в одной из четырех стандартных форм:

1) в форме Коши;

2) в пространстве состояний;

3) решенную относительно регулируемой величины - y(t);

4) в виде передаточной функций - W(p).

Форма Коши-матричная форма записи системы ДУ решенных исключительно относительно первой производной координат САР.

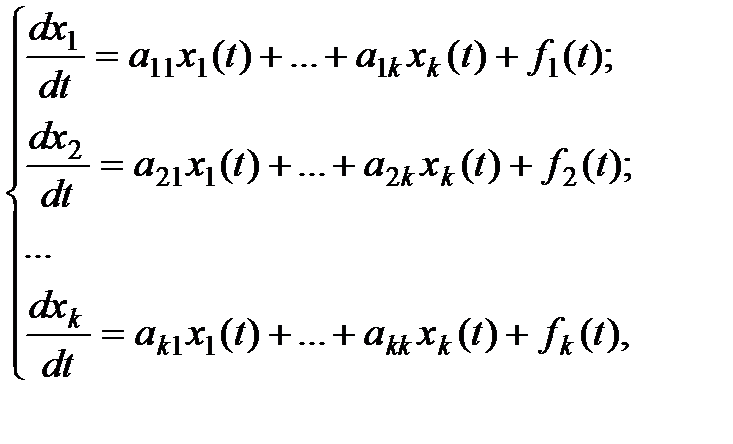(2.2)

где:

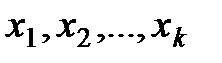- собственные координаты системы - ошибка системы x(t), воздействие на объект u(t), выходная координата - y(t) и т.д.;

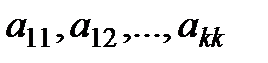- постоянные коэффициенты (если система не является зависимой от параметра) - суммы и произведения постоянных времени 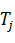, коэффициентов усиления ;

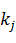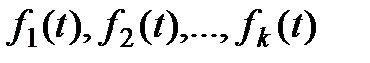- внешние координаты - задающие g(t) и возмущающие f(t) воздействия.

Форма Коши применяется в теории управления не часто; удобна, если для расчетов использовать классические математические пакеты (MathCAD, MATLAB и т.д.); используется при построении аналоговых вычислительных моделей матричного типа (например, моделей на операционных усилителях).

Пространство состояний (ABCD-форма)-матричная форма записи системы ДУ САР адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений связывающих внутренние координаты САР с выходной(ыми). Применяется для описания САР большого порядка, как правило, с несколькими входами/выходами и с перекрестными связями.

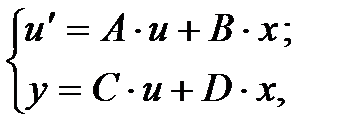(2.3)

где:

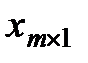- вектор входных переменных;

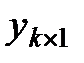- вектор выходных переменных;

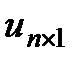- вектор переменных состояния (фазовых координат системы);

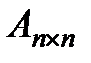- матрица коэффициентов системы;

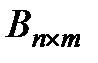- матрица входных коэффициентов (матрица управления);

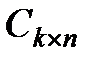- матрица выходных коэффициентов;

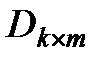- матрица коэффициентов пропорциональных каналов (матрица компенсации);

n - порядок системы; m - кол-во входов; k - кол-во выходов (m<n).

Форма "Пространство состояний" признана стандартом для программ математического моделирования VisSim, Simulink, и т.д., однако в большинстве случаев реализована в SISO-форме (с одним входом и одним выходом). Моделирующие программы для выполнения анализа (символьного или частотного) сводят любую модель пользователя к пространству состояний, заполняя в ходе первых шагов симуляции коэффициенты ABCD-матриц.

ДУ решенное относительно регулируемой величины y(t) - уравнение движения. Система ДУ (2.1) может быть преобразована к одному уравнению путем исключения промежуточных координат (обычно выходную координату выражают через координату задания). Результатом подобного преобразования является уравнение движения системы:

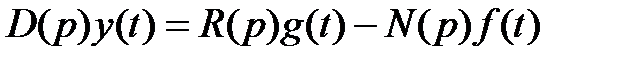, (2.4)

где:

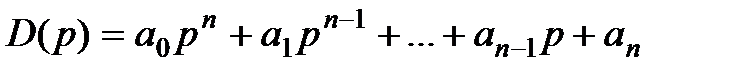- характеристический полином;

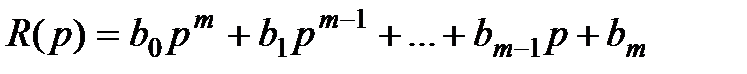– полином, определяющий влияние задающего воздействия g(t) на регулируемую координату у(t), причем его степень меньше степени характеристического полинома, т.е. m<n;

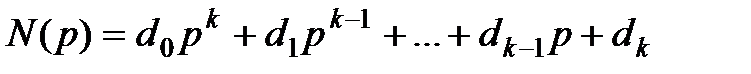– полином, определяющий влияние помехи f(t) на систему.

Передаточная функция (ПФ) - функция, связывающая один входной и один выходной сигналы САР. Является формой записи системы ДУ САР решённой относительно требуемой выходной координаты. Обычно ПФ записывается не для временного домена, а для домена Лапласа, связывая в этом варианте не сигналы (т.е. не функции времени), а их изображения.

ПФ получают из ДУ решенного относительно требуемой координаты системы (уравнение 2.4). Для чего правую часть уравнения делят на характеристический полином D(p). Отношения полиномов в правой части при возмущающих воздействиях и есть ПФ.

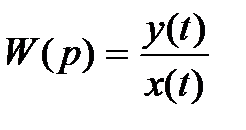, (2.5)

где y(t) – выходное значение САР, x(t) – входное значение САР.