Свойства поверхностного интеграла первого рода.
(они аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода).
1) Линейность. 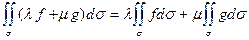
2) Аддитивность 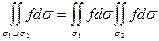
3) 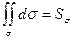 - площадь поверхности.
- площадь поверхности.
4) Если 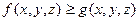 , то
, то 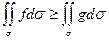 (если
(если 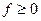 , то
, то 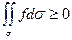 ),
),
5) Теорема об оценке.Если 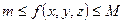 , то
, то 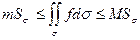 ,
,
6) Теорема о среднем. Пусть функция 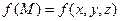 непрерывна на кусочно-гладкой ограниченной поверхности
непрерывна на кусочно-гладкой ограниченной поверхности 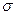 . Тогда на поверхности найдется точка С, такая что
. Тогда на поверхности найдется точка С, такая что 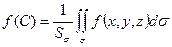
Доказательство. Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода (записью соотношений в интегральных суммах и предельным переходом). Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.
Теорема об оценке следует из свойств 3, 4.
Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.
Дата добавления: 2017-11-21; просмотров: 1154;











