Векторное произведение векторов
Если с заданием трёх векторов указано, какой из них считается первым, какой вторым и какой третьим, то говорят, что задана упорядоченная тройка векторов.
Упорядоченная тройка векторов 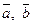 и
и 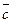 называется правой, если кратчайший поворот от первого вектора ко второму виден совершающимся против часовой стрелки, если смотреть с конца третьего вектора (рис.28). В противном случае тройка векторов называется левой.
называется правой, если кратчайший поворот от первого вектора ко второму виден совершающимся против часовой стрелки, если смотреть с конца третьего вектора (рис.28). В противном случае тройка векторов называется левой.
 | |||
 | |||

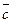
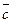
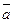


 правая
правая  левая
левая
тройка тройка
Рис.28
Векторным произведением двух векторов 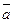 и
и 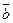 называется вектор
называется вектор 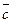 , обозначаемый символом
, обозначаемый символом 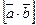 или
или 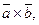 который определяется следующими тремя условиями:
который определяется следующими тремя условиями:
1. Модуль векторного произведения 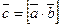 равен произведению модулей векторов
равен произведению модулей векторов 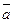 и
и 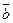 на синус угла между ними:
на синус угла между ними:
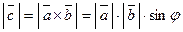 (4.26)
(4.26)
где 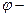 угол между векторами
угол между векторами 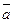 и
и 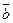 .
.
2. Вектор 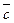 =
= 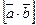 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов 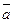 и
и 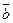 , т.е.
, т.е. 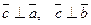 .
.
3. Вектор 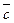 направлен таким образом, чтобы смотря в направлении от конца вектора
направлен таким образом, чтобы смотря в направлении от конца вектора 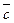 на плоскость векторов
на плоскость векторов 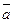 и
и 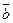 кратчайший поворот от
кратчайший поворот от 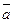 к
к 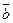 был виден против хода часовой стрелки.
был виден против хода часовой стрелки.
Свойства векторного произведения:
1. При перестановке местами сомножителей векторное произведение меняет свой знак:
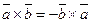
2. Векторное произведение подчиняется распределительному закону:
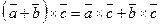
3. Векторное произведение подчиняется сочетательному закону по отношению к скалярному множителю:
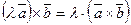 .
.
4. Если векторы 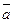 и
и 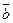 коллинеарны, то их векторное произведение равно нулю.
коллинеарны, то их векторное произведение равно нулю.
5. Векторные произведения ортов
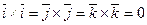
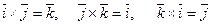 ,
,
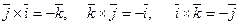
6. Модуль векторного произведения двух векторов 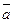 и
и 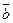 равен площади параллелограмма построенного на этих векторах:
равен площади параллелограмма построенного на этих векторах:
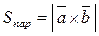
Из этой формулы имеем:
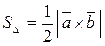
Данные формулы выражают геометрический смысл векторного произведения векторов.
Пример. Известно, что 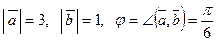 . Требуется найти: а)
. Требуется найти: а) 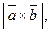 б)
б) 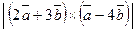 .
.
Решение. а) По формуле (4.26) имеем:
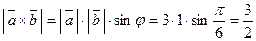 .
.
б) Используя свойства векторного произведения, будем иметь:
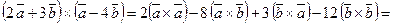
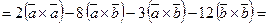
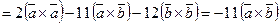
Поэтому,
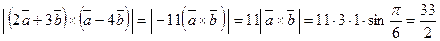 .
.
Дата добавления: 2017-10-04; просмотров: 1478;











