Лекция 7. Поверхностные интегралы.

Задача о массе поверхности.

Задача о массе поверхности приводит нас к поверхностному интегралу 1 рода, точно так же, как задача о массе кривой привела нас к криволинейному интегралу первого рода.

Пусть в каждой точке кусочно-гладкой поверхности s задана поверхностная плотность f(x, y, z).

1. Введем разбиение s на элементарные области Ds_i – элементы разбиения так, чтобы они не имели общих внутренних точек ( условие А).

2. Отметим точки M_i на элементах разбиения Ds_i. Вычисляем f (M_i) = f (x_i, y_i, z_i) и считаем плотность постоянной и равной f (M_i) на всем элементе разбиения Ds_i..Приближенно вычислим массу ячейки разбиения как f (M_i) Ds_i . Приближенно вычислим массу поверхности s, просуммировав массы ячеек (составим интегральную сумму) 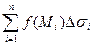. В интегральной сумме 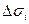- это площадь поверхности элементарной ячейки. Здесь, как и ранее, традиционно употребляется одно и то же обозначение для самой элементарной ячейки и для ее площади.

3. Измельчаем разбиение и переходим к пределу в интегральной сумме при условии 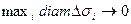(условие B). Получаем поверхностный интеграл первого рода, который равен массе поверхности (если только f(M_i)>0 на поверхности).

= .

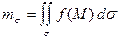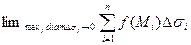Теорема существования. Пусть функция 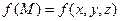непрерывна на кусочно-гладкой ограниченной поверхности 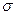. Тогда поверхностный интеграл первого рода существует как предел интегральных сумм.

= .

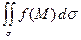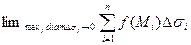Замечание. Интеграл (как предел интегральных сумм) не зависит:

1) от выбора разбиения поверхности (лишь бы выполнялось условие А),

2) от выбора отмеченных точек на элементах разбиения,

3) от способа измельчения разбиения (лишь бы выполнялось условие В).