Лекция 4. Приложения тройного интеграла.

Замена переменных в тройном интеграле.

Теорема. Пусть с помощью непрерывных функций x = x(u, v, w), y = y(u, v, w), z =z(u, v, w) имеющих непрерывные частные производные установлено взаимно однозначное соответствие пространственно односвязных ограниченных, замкнутых областей D_xyz, D_uvw с кусочно-гладкой границей. Тогда

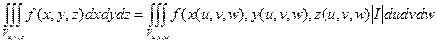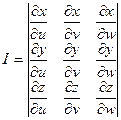, где - якобиан (определитель Якоби).

Теорема приведена без доказательства.

Цилиндрическая система координат.

	M

Вводятся цилиндрические координаты r, j, h. x = r cosj, y = r sinj, z = h. Вычислим якобиан

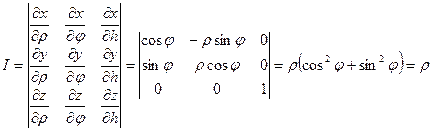
Пример Вычислить объем пространственного тела, заключенного между цилиндрической поверхностью 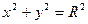и эллиптическим параболоидом . .

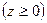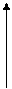
Сферическая система координат.

j x j q r z y

Сферические координаты j, r, q. x = r sinq cosj y= r sinq sinj z = r cosq. Вычислим якобиан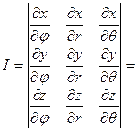

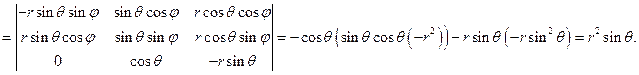
Пример. Найти массу части шара (с центром в начале координат, радиусом R), находящейся в первом октанте, если плотность вещества шара в каждой точке шара пропорциональна расстоянию этой точки от оси OZ.