Равновесие плазмы в магнитном поле

Подобно тому как в механике обычной жидкости простейшим случаем является гидростатика, т. е. раздел гидродинамики, изучающий равновесие жидкой или газообразной среды, в магнитной гидродинамике плазмы можно выделить раздел о равновесии плазмы в магнитном поле. В таких состояниях левая часть магнитогидродинамического уравнения Эйлера, описывающая инерцию плазмы, полагается равной нулю, и в результате получается уравнение

(15.1)

означающее, что сумма объемных сил, действующих на плазму, равна нулю в любой точке внутри плазмы.

Первым следствием условия равновесия плазмы (15.1) является постоянство ее давления вдоль силовых линий магнитного поля, так как [j×H]⊥H. В произвольном случае магнитное поле может иметь довольно сложный характер и свойства равновесного состояния плазмы оказываются непростыми. Задачи такого рода имеют важное значение в проблеме управляемого термоядерного синтеза. Здесь же мы рассмотрим простейший случай равновесия плазмы в магнитном поле с прямолинейными и параллельными друг другу силовыми линиями магнитного поля, иначе говоря, равновесие плазмы в продольном магнитном поле. Магнитное поле имеет только одну компоненту H_z, которая является функцией координат х и у (в плоскости, перпендикулярной к полю). В этом случае условие равновесия принимает вид

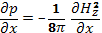
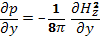(15.2)

Следовательно,

(15.3)

Это соотношение показывает, что магнитное давление H²/8πза пределами области, занятой плазмой, больше, чем внутри нее, на величину p_max. Максимальное давление, при котором плазма может удерживаться полем заданной напряженности H₀, определяется из условия

(15.4)

Видно, что магнитное поле внутри плазмы оказывается меньше внешнего поля; это следствие того, что плазма представляет собой диамагнетик. В этом случае плазма должна полностью вытеснять поле из занимаемой ею области пространства.

До сих пор, говоря о равновесии плазмы в магнитном поле, мы использовали лишь одно из уравнений магнитной гидродинамики — уравнение Эйлера, в котором считали du/dt=0. Выясним, совместимо ли это допущение с остальными уравнениями магнитной гидродинамики. Исходя из уравнения

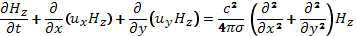(15.5)

приходим к выводу о неизбежности диффузии магнитного поля внутрь объема, занимаемого плазмой, т. е. в область более слабого поля. Таким образом, магнитное поле, вообще говоря, будет изменяться во времени. Но тогда давление плазмы, жестко связанное с магнитным давлением условием равновесия (15.3), тоже должно меняться, т. е. будет происходить изменение распределения плазмы в пространстве. Этот встречный процесс также имеет диффузионный характер. Коэффициент диффузии плазмы, очевидно, имеет такой же порядок величины, как и , если давление плазмы сравнимо с давлением магнитного поля .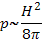

Уравнение, описывающее процесс диффузии плазмы в магнитном поле при , можно вывести следующим образом. Равновесие плазмы достигается в результате протекания тока плотностью

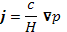(15.6)

Электрический ток связан с относительным движением электронов и ионов плазмы со скоростью j/en. Электрическое сопротивление такому току есть следствие силы трения между электронами и ионами плазмы:

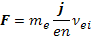(15.7)

где — время свободного пробега электронов по отношению к соударениям с ионами. Точно так же, как рассматривался дрейф заряженных частиц под действием произвольной силы F, можно говорить о дрейфе электронов и ионов под действием силы трения. Скорость такого дрейфа

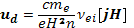(15.8)

Она одинакова для ионов и электронов, поскольку разные знаки зарядов ионов и электронов компенсируются взаимно противоположными направлениями сил трения. Поэтому в процессе такого дрейфа электрическая нейтральность плазмы не нарушается. Подставим теперь найденную скорость u_d движения плазмы под действием сил трения в уравнение, непрерывности. Получим уравнение диффузии

(15.9)

В результате проведенного анализа можно сделать вывод, что в реальном случае плазмы с конечной электропроводностью строгого равновесия не существует, так как скорость плазмы отлична от нуля. Это значит, что инерционный член в уравнении Эйлера, вообще говоря, не обращается в нуль и можно говорить лишь о приближенном выполнении условия равновесия. Это условие выполняется с тем большей точностью, чем меньше относительная величина инерционного члена.

Допустим, что τ_р — характерное время, за которое происходит изменение плотности плазмы. Тогда сделанное приближение справедливо при условии

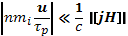
Подставляя u из (15.8), получаем

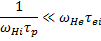(15.10)

Отсюда видно, что чем выше степень замагниченности плазмы, тем с большим правом можно говорить о ее равновесии.

Из рассмотренной картины диффузии плазмы в магнитном поле вытекает еще одно следствие: диффузия связана со столкновениями между частицами разного сорта — между электронами и ионами (столкновения между одинаковыми частицами в рассмотренном приближении не приводят к диффузии, так как не дают силы трения). Используя уравнение диффузии плазмы (15.9), нетрудно оценить время диффузии (т. е. время, за которое распределение плотности плазмы существенно изменится). Это время

(15.11)

Таким образом, данное равновесие плазмы имеет конечное время жизни порядка τ_р.

Полезно привести еще один вывод коэффициента диффузии плазмы поперек магнитного поля, рассматривая случайные блуждания частиц вследствие столкновений. За время одного свободного пробега τ_eiэлектрон в среднем испытывает одно кулоновское столкновение, в результате которого он смещается в плоскости, перпендикулярной к H, на расстояние порядка ларморовского радиуса r_He.При многократных столкновениях согласно статистическим законам складываются квадраты отдельных смещений. Поэтому за время t частица сместится перпендикулярно к H на расстояние

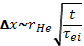(15.12)

Кроме того, среднее смещение при таком диффузионном процессе должно быть порядка
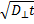. Следовательно,

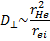(15.13)

Вследствие квазинейтральности плазмы скорость ее диффузии в направлении, перпендикулярном к H, должна практически совпадать со скоростью диффузии электронов, так как при сравнимых значениях температуры электроны из-за меньшей величины ларморовского радиуса блуждают поперек поля гораздо медленнее, чем ионы. Поэтому формула (15.13) дает оценку коэффициента диффузии для плазмы в целом. Среднее время между двумя столкновениями .

Поэтому

(15.14)

По порядку величины этот результат совпадает с найденным ранее коэффициентом диффузии (15.9).

В диффузию рассмотренного типа дают вклад только столкновения электронов с ионами, но не электронов между собой. Это обстоятельство может ускользнуть от внимания, если ограничиться лишь грубой моделью случайныхблуждений. Вот почему макроскопический подход, основанный на силе трения, особенно полезен. Он автоматически учитывает, что столкновения между электронами не создают средней силы трения, а следовательно, и диффузионного дрейфа.Очевидно, что теплопроводность плазмы в направлении, перпендикулярном к H, также должна резко снижаться при увеличении напряженности поля. В противоположность диффузии, которая обусловлена столкновениями между ионами и электронами, теплопередача в плазме поперек силовых линий происходит в основном в результате ион-ионных столкновений (если Т_i не слишком мало по сравнению с Т_е). Это объясняется тем, что интенсивность теплопередачи зависит от ширины той области, в пределах которой при наличии градиента температуры перемешиваются траектории частиц с различной тепловой энергией. Коэффициент теплопроводностив направлении, перпендикулярном к H, пропорционален квадрату ширины области перемешивания, а эта ширина по порядку величины сравнима с ларморовским радиусом. Поэтому теплопередача в основном идет через ионную компоненту .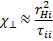

Отсюда видно, что коэффициент ионной теплопроводности в направлении, перпендикулярном к силовым линиям, уменьшается примерно в (ω_Hiτ_ii)²раз по сравнению с тем значением, которое он имеет в отсутствие магнитного поля. Коэффициент поперечной теплопроводности для водородной плазмы можно вычислить, пользуясь следующей формулой:

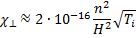(15.15)

В различных приложениях физики плазмы рассматриваются достаточно сложные типы равновесия плазмы в магнитном поле (так называемые магнитогидродинамические равновесные конфигурации). Однако и в таких произвольных случаях сохраняется основной вывод, сделанный здесь на примере магнитного поля, имеющего только одну компоненту: равновесие имеет условный характер, так как оно с течением времени разрушается из-за диффузии и теплоотвода. В сложных равновесных конфигурациях выражения для коэффициентов диффузии и теплопроводности плазмы поперек магнитного поля могут заметно отличаться от (15.14) и (15.15). Это можно понять, если вспомнить, насколько сложными могут быть дрейфовые траектории электронов и ионов в произвольных магнитных полях. В таких полях в качестве элементарного шага в схеме случайных блужданий частицы может входить величина, намного превышающая ларморовский радиус частицы. Некоторые эффекты такого типа, важные для исследований по управляемым термоядерным реакциям, рассмотрены в параграфе,посвященном токамаку.