Идеальная проводимость и дрейфовое движение

Во многих задачах от приближения магнитной гидродинамики можно перейти к еще более упрощенному способу рассмотрения плазмы, устремив проводимость σк бесконечности. Такое рассмотрение носит название приближения идеальной проводимости. При бесконечной проводимости сколь угодно малое электрическое поле вызывало бы бесконечный ток, что требовало бы бесконечно большой затраты энергии, и потому невозможно. Следовательно, в приближении идеальной проводимости электрическое поле в системе координат, связанной с плазмой (такую систему иногда называют сопутствующей), должно равняться нулю

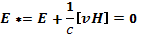(13.1)

или

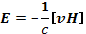(13.2)

Векторное произведение [vH] зависит только от составляющей скорости, перпендикулярной к магнитному полю, которую мы будем обозначать v_⊥. Поэтому выражение (13.2) можно записать в виде

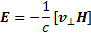(13.2а)

поскольку результат от этого не изменится. Таким образом, условие (13.2) накладывает определенное требование на скорость движения плазмы поперек магнитного поля v_⊥; скорость вдоль магнитного поля v_|| может иметь любое значение. Чтобы получить значение v_⊥, достаточно умножить выражение (13.2а) векторно на Н справа. Получаем

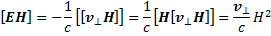(13.3)

так как скалярное произведение 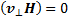. Из равенства (13.3)

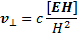(13.4)

В скрещенных магнитном и электрическом полях идеально проводящая среда должна двигаться со скоростью, определяемой формулой (13.4). Такое движение называется дрейфом, а скорость, выражаемая формулой (13.4), —дрейфовой скоростью. Когда мы будем рассматривать движение заряженных частиц в плазме, то ознакомимся еще с рядом разновидностей дрейфового движения. Но только для дрейфа в скрещенных магнитном и электрическом полях скорость дрейфа одной частицы совпадает со скоростью дрейфа плазмы как целого. Этот вид дрейфового движения называется электрическим дрейфом в отличие от других видов дрейфа, при которых частицы разных зарядов движутся, как мы увидим, в противоположных направлениях. Как видно из формулы (13.4), скорость электрического дрейфа направлена перпендикулярно к плоскости, в которой лежат векторы магнитного и электрического полей. В формуле (13.4) величина векторного произведения [ЕН] зависит только от составляющей электрического поля, перпендикулярной к магнитному; эту составляющую мы будем обозначать E_⊥. Поэтому формулу (13.4) можно записать в виде

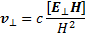(13.4a)

Параллельная магнитному полю составляющая электрического поля не влияет на скорость дрейфа плазмы как целого поперек поля; она вызывает ток, текущий вдоль магнитного поля. Величина дрейфовой скорости выражается как

(13.5)

Пользоваться выражением дрейфовой скорости в векторной форме нужно только для того, чтобы определить ее направление при данных направлениях магнитного и электрического полей. Из формулы (13.4а) следует, что если магнитное поле направлено к нам, а перпендикулярная к нему составляющая электрического поля вверх, то плазма должна дрейфовать вправо. При приближенном рассмотрении поведения плазмы в магнитном поле удобно пренебречь электрическим сопротивлением плазмы, т. е. рассматривать ее как идеально проводящую среду. Согласно только что сказанному, движение плазмы в этом приближении будет иметь дрейфовый характер. Поэтому такое приближение и называется дрейфовым приближением.

Вмороженное поле

Можно дать и другую физическую интерпретацию дрейфового движения идеально проводящей среды. Известно, что если проводник при своем движении пересекает силовые линии магнитного поля, то в нем возбуждается электродвижущая сила. В идеальном проводнике сколь угодно малая электродвижущая сила возбуждала бы бесконечный ток, что невозможно. Следовательно, идеальный проводник должен увлекать с собой магнитные силовые линии так, как если бы они были ё него «вморожены». Иными словами, идеально проводящая плазма движется так, как если бы ее частицы были «приклеены» к силовым линиям магнитного поля. Дадим количественную формулировку понятия вмороженного поля. Для этого воспользуемся уравнением Максвелла

(14.1)

и подставим в него значение электрического поля (13.2). В результате подстановки получим

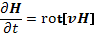(14.2)

Раскрываем ротор векторного произведения по формулам векторного анализа и, учитывая, что divH = 0, получаем

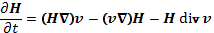(14.3)

Можно ввести субстанциональную, или лагранжеву, производную, которая выражает изменение рассматриваемой величины для выбранного движущегося элемента вещества

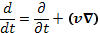(14.4)

Тогда выражение (14.3) запишется как

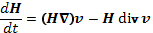(14.5)

Воспользуемся теперь известным из гидродинамики уравнением непрерывности (или неразрывности)

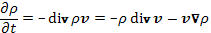(14.6)

или

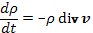(14.7)

Если из уравнения (14.7) выразить divv и подставить в уравнение (14.5), то получим

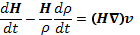(14.8)

Левую часть равенства можно теперь выразить через производную от величины Н/ρ. Для этого заметим, что

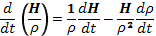(14.9)

откуда

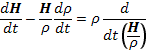(14.10)

Таким образом, уравнение (14.8) можно представить в виде

(14.11)

Рассмотрим сначала простейший случай, когда скорость меняется только в направлении, перпендикулярном к магнитному полю. Тогда правая часть уравнения (12.11) обращается в нуль и, следовательно,

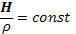(14.12)

Постоянство скорости вдоль силовой линии означает, что силовая линия не растягивается и не сжимается. При этом вмороженность поля заключается в том, что густота силовых линий, т. е. напряженность поля, меняется пропорционально плотности вещества. Рассмотренный простейший случай имеет место, в частности, при плоском (одномерном) сжатии плазмы поперек магнитного поля. При этом напряженность магнитного поля возрастает пропорционально плотности, а магнитное давление Н²/8π —пропорционально квадрату плотности. Эффективный показатель адиабаты для магнитного давления γ_⊥= 2. При плоском сжатии поперек поля магнитное давление возрастает быстрее, чем давление идеального газа.

Противоположная картина будет наблюдаться при плоском сжатии вдоль магнитнго поля. В этом случае уравнение (14.11) примет вид

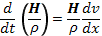
а уравнение (14.7) получит вид

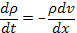
где х — координата, направленная вдоль поля. Из сопоставления этих двух выражений следует

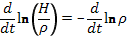
откуда Н/ρменяется пропорционально 1/ρ, т. е. Н = const. Таким образом, при плоском сжатии плазмы вдоль магнитного поля напряженность поля и магнитное давление остаются постоянными: γ_||=0. Так и должно быть согласно представлению о вмороженном поле: при плоском сжатии вдоль поля силовые линии только сокращаются в длину, но не сгущаются.

Для рассмотрения общего случая следует ввести понятие длины «вещественной линии», ограниченной с концов выбранными элементами вещества. Пусть концы линии движутся со скоростями v₁ и v₂. Изменение со временем длины вещественной линии

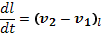
где индекс l означает проекцию вектора на направление l. Для векторного элемента длины

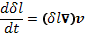(14.13)

Это выражение отличается от уравнения (14.11) только заменой Н/ρна δl. Отсюда следует, что при произвольных движениях плазмы вектор Н/ρ должен меняться пропор-пропорционально δl. В частности, если δlвыбрано первоначально в направлении Н, то их направления и в дальнейшем будут совпадать. Таким образом, получается общая количественная формулировка понятия вмороженного поля

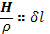(14.14)

где δl — длина элемента вещественной линии, направленной вдоль силовой линии магнитного поля.

Пользуясь тем, что, как доказано, силовые линии вморожены в вещество, l можно называть длиной силовой линии. Тогда формулу (14.14) можно понимать так: если силовые линии растягиваются, то величина Н/ρ возрастает, если они сокращаются, то Н/ρ уменьшается.

Найденные выше простейшие результаты легко получить из формулы (14.14). При плоском сжатии поперек поля длина силовых линий не меняется, вследствие чего Н меняется пропорциональноρ. При плоском сжатии вдоль поля длина силовых линий меняется обратно пропорционально плотности, а Н остается постоянным.

Соотношение (14.14) позволяет рассмотреть и более сложный случай изотропного (подобного или сферического) сжатия. В этом случае значение длины есть корень кубический из объема, откуда

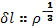
Подстановка в формулу (14.14) дает

Магнитное давление:

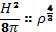
Эффективный показатель адиабаты для магнитного давления при изотропном сжатии: γ_м = 4/3. Как известно, такое же значение показателя адиабаты и для давления электромагнитного излучения.

Характер нарастания магнитного поля зависит только от симметрии сжатия для любых конфигураций поля, в том числе и для неупорядоченных турбулентных полей. Закон нарастания магнитного поля при изотропном сжатии имеет большое значение в астрофизике, в частности в теории образования звезд посредством гравитационной конденсации космической плазмы. При этом напряженность вмороженных в плазму полей возрастает пропорционально плотности в степени 2/3, и приходится вводить специальные механизмы вытеснения поля, чтобы объяснить, почему образующиеся звезды не обладают колоссальными магнитными полями. Все изложенные результаты, касающиеся вмороженного поля, справедливы только для идеально проводящей плазмы, т. е. в дрейфовом приближении. Границы применимости дрейфового приближения и отступления от него связаны уже с конечной проводимостью плазмы.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 1, §§3-5)