Вывод формулы Саха из квазиклассической статистики

Согласно квазиклассической статистике, вероятность нахождения частицы в состоянии с энергией ℰ выражается формулой Больцмана

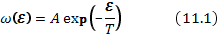
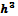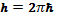где Т — температура в энергетических единицах. Число частиц с энергией ℰ равно вероятности, умноженной на число состояний. Для частицы, не имеющей внутренних степеней свободы, число состояний равно числу элементарных ячеек фазового пространства объемом , где — обычная постоянная Планка. Для электрона с импульсом между 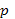и 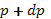фазовый объем

где V — обычный объем. Число электронов в этом объеме

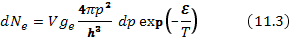
Здесь 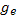— статистический вес, т. е. число состояний с одинаковой энергией, различающихся внутренними степенями свободы. Рассматривая равновесие электронов с атомами, мы можем за нуль энергии считать энергию электрона в атоме. Тогда энергия свободного электрона с импульсом p

где J — энергия ионизации атома (ее часто называют потенциалом ионизации и выражают в электронвольтах). Число свободных электронов на один атом в определенном квантовом состоянии найдется интегрированием по всем значениям импульса

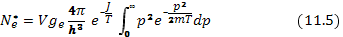
Интеграл берется по формуле

В данном случае 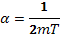,вследствие чего выражение (11.5) дает

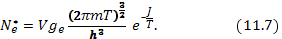
Чтобы получить полное число электронов 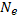, этот результат надо умножить на число атомов в одном квантовом состоянии 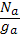, где 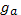— полный статистический вес нейтрального атома. После этого

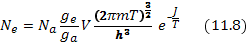
Квазиклассический вывод недостаточно строг, так как приняты два не вполне очевидных допущения. Во-первых, мы считали, что интегрирование выражения (11.3) дает число электронов на один атом в определенном квантовом состоянии. Во-вторых, в равновесии ионизации участвуют также и ионы, и, чтобы учесть это, нужно за V принять объем, приходящийся на один ион в определенном квантовом состоянии:

где 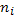— число ионов в единице объема; 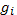— статистический вес иона. Подстановка формулы (11.9) в выражение (11.8) дает формулу Саха в окончательном виде

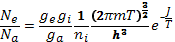
Отношение полных чисел частиц N равно отношению концентраций n, что позволяет записать формулу Саха в симметричном виде

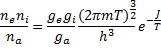
где размерность концентраций в см^-3. Квазиклассический вывод формулы Саха физически нагляден, но содержит допущения, которые строго не обоснованы. Рассмотрение же равновесия ионизации как частного случая химического равновесия позволяет вывести ту же формулу общим методом химической термодинамики без либо нестрогих допущений.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 2, §§2-5)

7. Гидродинамическое описание плазмы (МГД-приближение). Магнитная гидродинамика. МГД-уравнения. Вмороженность магнитного поля. Равновесие плазмы. Условия равновесия. Равновесие цилиндрического столба. θ-пинч. Z-пинч.Бессиловые конфигурации. Тороидальная плазма в поле с замкнутными силовыми линиями. Ловушка с гофрированным магнитным полем. Двухжидкостная магнитная гидродинамика. Эффект Холла. Стационарный ток при эффекте Холла. Равновесие плазмы в перекошенном магнитном поле. Диффузия плазмы. Плазма в однородном магнитном поле. Диффузия плазмы в торе. Амбиполярная диффузия слабоионизированной плазмы. Бомовскаядиффузия.