Проводимость плазмы

Для простейшего случая постоянного тока в однородной плазме уравнение обобщенного закона Ома (16.18) принимает вид

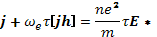(17.1)

где

(17.2)

электронная циклотронная частота; h — единичный вектор в направлении магнитного поля.

При отсутствии магнитного поля или для составляющей тока вдоль его направления векторное произведение [jH] выпадает, и из уравнения (17.1) получается нормальная или продольная проводимость плазмы

(17.3)

Для нахождения поперечной проводимости расписываем уравнение (17.1) в составляющих. Если направить ось z вдоль магнитного поля, то

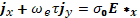(17.4)

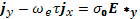(17.5)

Поперечная проводимость плазмы есть величина тензорная. Проще всего выразить соотношения (17.3)—(17.5) с помощью тензора сопротивления R, определяемого соотно- соотношением

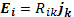(17.6)

Компоненты этого тензора образуют таблицу (матрицу):

(17.7)

Обычно принято вместо тензора сопротивления пользоваться тензором проводимости, который определяется равенством

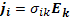(17.8)

Чтобы найти компоненты этого тензора, нужно найти матрицу, обратную (17.7), т. е. решить систему уравнений (17.4)—(17.5) относительно составляющих тока. В данном случае достаточно умножить одно из уравнений на 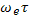, прибавить ко второму или вычесть из него, чтобы получить

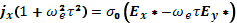(17.9)

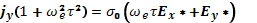(17.10)

Отсюда тензор проводимости однородной плазмы для постоянного тока имеет вид:

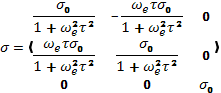(17.11)

В явном виде составляющие тока выражаются формулами:

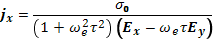(17.12)

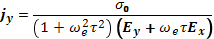(17.13)

(17.14)

Для замагниченнои плазмы 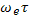— большое число. В этом случае поперечная проводимость должна быть гораздо меньше продольной и уменьшаться обратно пропорционально квадрату циклотронной частоты, т. е. квадрату напряженности магнитного поля. Ток должен течь не только вдоль электрического поля, но и поперек него (холл-эффект), причем в замагниченнои плазме при скрещенных полях ток поперек электрического поля (холловский ток) должен быть гораздо больше, чем ток вдоль электрического, но поперек магнитного поля, и уменьшаться только как первая степень напряженности магнитного поля. В реальных условиях проводимость плазмы сильно осложняется пространственной неоднородностью, вызывающей электрические поля поляризации, а также дрейфовые токи и ток намагничивания.

(источник: Д.А. Франк-Каменецкий, Лекции по физике плазмы, гл. 1, §§7-8)