Неравенство Клаузиуса. Закон возрастания энтропии

Напомним, что согласно второй теореме Карно (см. § 10), КПД h любой тепловой машины, проходящей цикл с использованием двух тепловых резервуаров, не может превышать КПД цикла Карно (h £ h_к). Обозначим температуры резервуаров Т_Н и Т_Х (Т_Н > Т_Х), а количества тепла, получаемые от них рабочим телом Q_Н и Q_Х соответственно (Q_Х < 0). Тогда h£ h_к, или

.

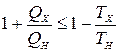Отсюда следует, что

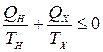, (15.1)

т.е. сумма приведенных количеств теплоты в рассматриваемом цикле меньше или равна нулю. Соотношение (15.1) представляет собой частный случай неравенство Клаузиуса для цикла, в котором рабочее тело обменивается теплом с двумя тепловыми резервуарами.

Для произвольного цикла, в котором рабочее тело контактирует с большим числом тепловых резервуаров, неравенство Клаузиуса можно получить, разбивая цикл близкими друг к другу адиабатами на большое количество элементарных циклов, аналогично тому, как было получено равенство Клаузиуса в §13. Записывая для малых циклов соотношения (15.1) и суммируя, получим неравенство Клаузиуса, справедливое для любого цикла:

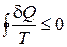. (15.2)

Здесь Т – температура теплового резервуара, от которого рабочее тело получает элементарное количество теплоты dQ. Когда все процессы в цикле обратимы, при каждом элементарном акте теплопередачи температуры рабочего тела и резервуара неотличимы, и неравенство (15.2) переходит в равенство Клаузиуса (13.3).

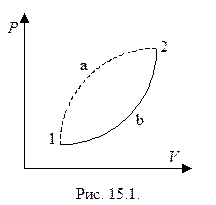Рассмотрим произвольный процесс 1-а-2 (обратимый или необратимый), переводящий систему из состояния 1 в состояние 2 (Рис. 15.1.). Вернемся в состояние 1, используя обратимый процесс 2-b-1. Запишем неравенство Клаузиуса для цикла 1-а-2-b-1:

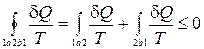. (15.3)

Для обратимого процесса 2-b-1 приведенное количество теплоты равно изменению энтропии

.

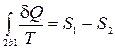Подставляя это выражение в неравенство (15.3), получим

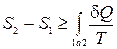. (15.4)

Таким образом, изменение энтропии в каком-либо процессе не может быть меньше приведенного количества теплоты. Неравенство (15.4) часто записывают в дифференциальной форме для бесконечно малых процессов

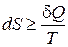. (15.5)

Если процессы обратимы, выражения (15.4) и (15.5) переходят в равенства.

Для процессов, происходящих в теплоизолированной системе, dQ = 0. Тогда из неравенств (15.4) и (15.5) следует закон возрастания энтропии: энтропия адиабатически изолированной системы не может убывать. При обратимых процессах она остается неизменной, при необратимых процессах возрастает.

Чтобы найти изменение энтропии в необратимом процессе следует рассмотреть какой-либо обратимый процесс с теми же начальным и конечным состояниями, и рассчитать для него приведенное количество тепла.

В качестве примера найдем изменение энтропии идеального газа при расширении в пустоту от объема V₁ до объема V₂ в теплоизолированном сосуде. Так как в этом процессе газ работу не совершает и не получает тепла, его внутренняя энергия не меняется. Для идеального газа неизменность внутренней энергии означает постоянство температуры Т. Чтобы вычислить изменение энтропии газа рассмотрим квазистатический изотермический процесс, в котором газ находится в тепловом контакте с нагревателем, имеющим температуру Т. Медленно уменьшая давление на газ можно увеличить его объем от V₁ до V₂. При этом газ получит от нагревателя количество тепла Q, за счет которого совершит работу А.

.

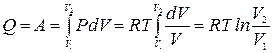Отсюда

.

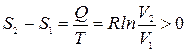Такое же возрастание энтропии будет при расширении в пустоту, хотя газ тепла не и получает. Увеличение энтропии вызвано необратимостью процесса.