Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
Свойство 2.7. Определитель матрицы Грама от линейно зависимой системы векторов равен 0.
Доказательство. Пусть система векторов 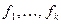 - линейно зависима. Тогда, либо система содержит нулевой вектор, и утверждение в этом случае очевидно, либо найдется вектор
- линейно зависима. Тогда, либо система содержит нулевой вектор, и утверждение в этом случае очевидно, либо найдется вектор 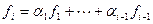 , линейно выражающийся через предыдущие векторы системы. В матрице Грама
, линейно выражающийся через предыдущие векторы системы. В матрице Грама 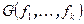 вычтем из i-ой строки, предыдущие строки с коэффициентами
вычтем из i-ой строки, предыдущие строки с коэффициентами 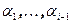 . Определитель матрицы Грама при этом не изменится, а i-ая строка станет равной нулю. Определитель матрицы с нулевой строкой равен нулю, а, значит, и определитель матрицы Грама равен нулю.
. Определитель матрицы Грама при этом не изменится, а i-ая строка станет равной нулю. Определитель матрицы с нулевой строкой равен нулю, а, значит, и определитель матрицы Грама равен нулю.
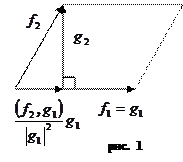 Рассмотрим геометрический смысл матрицы Грама от линейной не зависимой системы векторов
Рассмотрим геометрический смысл матрицы Грама от линейной не зависимой системы векторов 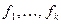 . Если k=1, то
. Если k=1, то 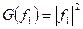 - квадрат длины вектора. Если k>1, то применим к системе векторов
- квадрат длины вектора. Если k>1, то применим к системе векторов 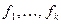 процесс ортогонализации и построим ортогональную систему векторов
процесс ортогонализации и построим ортогональную систему векторов 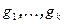 . Обозначим через P матрицу перехода от системы
. Обозначим через P матрицу перехода от системы 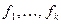 к системе
к системе 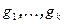 . Эта матрица имеет треугольный вид, а на ее главной диагонали стоят 1, и ее определитель равен 1. Кроме того,
. Эта матрица имеет треугольный вид, а на ее главной диагонали стоят 1, и ее определитель равен 1. Кроме того, 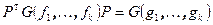 и, следовательно, определители матриц Грама равны. Поскольку система векторов
и, следовательно, определители матриц Грама равны. Поскольку система векторов 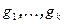 - ортогональна, то матрица Грама от этой системы векторов – диагональная, и ее определитель равен произведению квадратов длин векторов этой системы. Таким образом, установлено равенство
- ортогональна, то матрица Грама от этой системы векторов – диагональная, и ее определитель равен произведению квадратов длин векторов этой системы. Таким образом, установлено равенство 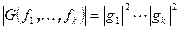 . Рассмотрим случай k=2. Тогда
. Рассмотрим случай k=2. Тогда 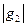 равна длине высоты параллелограмма, опущенного на сторону
равна длине высоты параллелограмма, опущенного на сторону 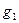 (см. рис. 1). Следовательно, произведение
(см. рис. 1). Следовательно, произведение 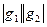 равно площади параллелограмма натянутого на векторы
равно площади параллелограмма натянутого на векторы 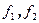 , а определитель матрицы Грама
, а определитель матрицы Грама 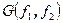 равен квадрату площади этого параллелограмма. Если k=3, то вектор
равен квадрату площади этого параллелограмма. Если k=3, то вектор 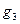 является ортогональной составляющей вектора
является ортогональной составляющей вектора 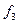 к плоскости, натянутой на векторы
к плоскости, натянутой на векторы 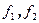 . Следовательно, определитель матрицы Грама от трех векторов равен квадрату объема параллелепипеда, натянутого на векторы
. Следовательно, определитель матрицы Грама от трех векторов равен квадрату объема параллелепипеда, натянутого на векторы 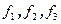 . Поскольку все рассуждения обобщаются на произвольную размерность, то тем самым установлено свойство.
. Поскольку все рассуждения обобщаются на произвольную размерность, то тем самым установлено свойство.
Свойство 2.8 Определитель матрицы Грама от системы векторов равен 0, если система линейно зависима, и квадрату объема k-мерного параллелепипеда натянутого на векторы 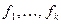 иначе.
иначе.
Расстояние.
Расстоянием между множествами X и Y называется 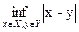 .
.
Расстояние между линейными многообразиями достигается на общем перпендикуляре.
Расстояние между линейным подпространством 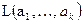 и точкой
и точкой 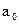 равно
равно 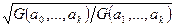 .
.
Расстояние между точкой x и гиперплоскостью ax=b равно 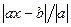 .
.
Дата добавления: 2016-07-27; просмотров: 2679;











