неберущиеся» интегралы

Не для всякой функции первообразная (если она существует) может быть записана через элементарные функции, например

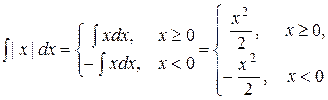
т.е. первообразная представляет собой кусочно-аналитическая функция.

Но существует целый ряд функций, для которых первообразную нельзя записать даже в виде кусочно-элементарной (ступенчатой) функции, например

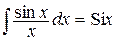– интегральный синус;

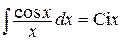– интегральный косинус;

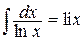– интегральный логарифм,

а также интегралы 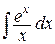, 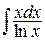(сравните с ).

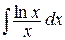К не берущимся относится и интеграл 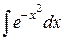(сравните 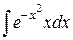). Одна из первообразных функции 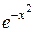играет важнейшую роль в теории вероятностей – функция Ф(х)= 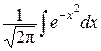, Ф(0) = 0 – эта функция называется функцией Лапласа. Для ее значений существуют подробные таблицы, изучены ее свойства. График этой функции имеет вид

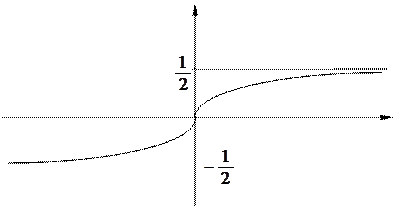
Рассмотрим интеграл вида

,

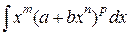где т, п, р – рациональные числа. Такой интеграл называется интегралом от дифференциального бинома. П.Л.Чебышев доказал, что этот интеграл может быть вычислен в конечном виде только в трех случаях:

а) р – целое (интегрируется подстановкой х = t^k , где k – общий знаменатель дробей т и п);

б) 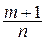– целое (замена 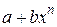= t^k, где k –знаменатель дроби р);

в) 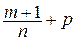– целое (замена 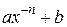= t^k, где k –знаменатель дроби р).

Во всех остальных случаях интеграл от дифференциального бинома в конечном виде не берется.