Интегрирование иррациональных функций

Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те иррациональные функции, для которых это возможно.

1) Интеграл вида 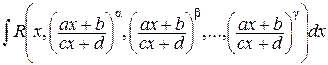, где a, b,..., g – обыкновенные дроби, приводится к интегралу от рациональной функции с помощью подстановки

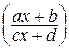= t^k , где k общий знаменатель дробей a, b, ..., g.

В частности, если a = d =1, b = c =0, рассмотренный интеграл имеет вид

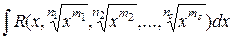
и к нему применима подстановка х = t^k, где k общий знаменатель дробей .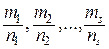

Если d =1, c =0, то интеграл имеет вид

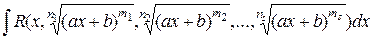
и ему соответствует подстановка 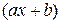= t^k, где где k общий знаменатель дробей .

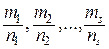Пример3.

.

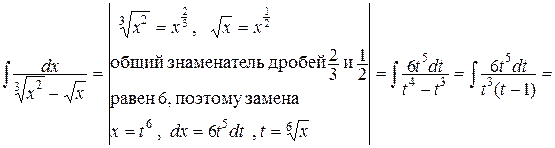
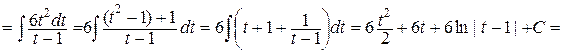
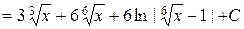2)Для вычисления интегралов, не содержащих других иррациональностей, кроме корня квадратного из суммы или разности квадратов, удобно использовать тригонометрические подстановки:

а) 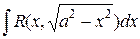– используется подстановка х = acost , dx = –asintdt (или x = sint, dx = costdt);

б) 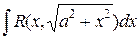– рекомендуется подстановка x = tgt, dx = ;

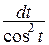в) 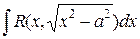– рекомендуется подстановка 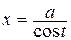(или ), .

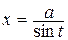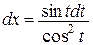г) 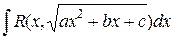сводится к интегралам вида а) – в), если в подкоренном выражении выделить полный квадрат

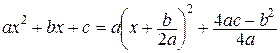
и сделать замену 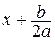= t.